Question

定义在R上的偶函数f（x）在x≥0时的图象是如图所示的抛物线的一部分．
（1）请补全函数f（x）的图象；
（2）写出函数f（x）的表达式（不要过程）；
（3）若方程f（x）=a恰有2个不同的解，求实数a的取值范围．

Answer 1

考点：分段函数的应用

专题：作图题,函数的性质及应用

分析：（1）由偶函数的图象关于y轴对称，即可得到f（x）的图象；
（2）根据顶点坐标和x轴的交点坐标，即可得到函数的解析式；
（3）作出直线y=a，方程f（x）=a恰有2个不同的解，即为直线y=a和f（x）的图象有两个交点．通过图象即可得到a的范围．

解答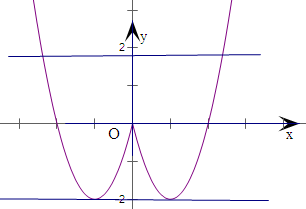： 解：（1）定义在R上的偶函数f（x），
则图象关于y轴对称，
如右图，即为f（x）的图象；
（2）f（x）=

2x2-4x，x≥0 2x2+4x，x＜0

；
（3）作出直线y=a，方程f（x）=a恰有2个不同的解，即为直线y=a和f（x）的图象有两个交点．
由图可知，a=-2或a＞0．

点评：本题考查分段函数及运用，考查分段函数的图象和函数解析式，以及直线与曲线的交点个数，属于中档题．