题目内容
5．已知△ABC三个内角A、B、C所对的边分别为a、b、c，且3sinA=a，sinB=$\frac{3}{4}$，则b等于（ ）| A． | $\frac{9}{4}$ | B． | 2 | C． | 3 | D． | 4 |
分析 直接利用正弦定理化简可得答案．
解答 解：3sinA=a，sinB=$\frac{3}{4}$，
由正弦定理$\frac{a}{sinA}$=$\frac{b}{sinB}$，
则有：$\frac{3sinA}{sinA}=\frac{b}{\frac{3}{4}}$．
得：b=$\frac{9}{4}$．
故选：A．
点评 本题考查三角形的正弦定理的运用，考查运算能力，属于基础题．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
1．若复数$\frac{a+i}{1+2i}（{a∈R}）$为纯虚数，其中i为虚数单位，则a=（ ）
| A． | 2 | B． | $\frac{1}{2}$ | C． | -2 | D． | $-\frac{1}{2}$ |
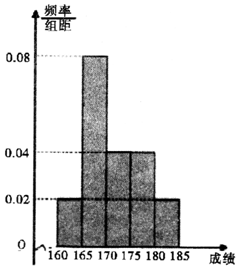近期中央电视台播出的《中国诗词大会》火遍全国．某选拔赛后，随机抽取100名选手的成绩，按成绩由低到高依次分为第1，2，3，4，5组，制成频率分布直方图如图所示：
设铁路AB长为100，BC⊥AB，且BC=30，为将货物从A运往C，现在AB上距点B为x的点M处修一公路至C，已知单位距离的铁路运费为2，公路运费为4．