题目内容
9.在[0,1]上任取两数x和y组成有序数对(x,y),记事件A为“x2+y2<1”,则P(A)=$\frac{π}{4}$.分析 由题意,本题是几何概型的概率求解,只要求出满足条件的区域面积,利用面积比求得概率.
解答 解:在[0,1]上任取两数x和y组成有序数对(x,y),对应的区域是边长为1的正方形,面积为1,
记事件A为“x2+y2<1”,在已知条件下,对应区域是半径为1 的$\frac{1}{4}$圆,
由几何概型的公式得到P(A)=$\frac{\frac{1}{4}π×{1}^{2}}{1}=\frac{π}{4}$;
故答案为:$\frac{π}{4}$
点评 本题考查了几何概型的概率求法;关键是明确事件的对应区域,利用面积比求得概率.

练习册系列答案
相关题目
20. 有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过38,则该塔形中正方体的个数至少是( )
有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过38,则该塔形中正方体的个数至少是( )
 有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过38,则该塔形中正方体的个数至少是( )
有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过38,则该塔形中正方体的个数至少是( )| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |
14.“sinαcosβ+cosαsinβ=$\frac{1}{2}$”是“$α+β=2kπ+\frac{π}{6}$,k∈Z”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
1.函数f(x)=$\sqrt{1-x}$+lg(x+2)的定义域为( )
| A. | (-2,1) | B. | [-2,1] | C. | (-2,+∞) | D. | (-2,1] |
19.设集合A={x|x<0},B={x|x2≤1},则A∩B等于( )
| A. | (-1,0) | B. | [-1,0) | C. | (-∞,-1] | D. | (-∞,-1) |
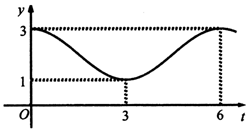 某工厂有甲、乙两生产车间,其污水瞬时排放量y(单位:m3/h )关于时间t(单位:h)的关系均近似地满足函数y=Asin(ωt+φ)+b(A>0,ω>0,0<φ<π),其图象如下:
某工厂有甲、乙两生产车间,其污水瞬时排放量y(单位:m3/h )关于时间t(单位:h)的关系均近似地满足函数y=Asin(ωt+φ)+b(A>0,ω>0,0<φ<π),其图象如下: