Question

17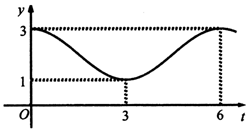．某工厂有甲、乙两生产车间，其污水瞬时排放量y（单位：m³/h ）关于时间t（单位：h）的关系均近似地满足函数y=Asin（ωt+φ）+b（A＞0，ω＞0，0＜φ＜π），其图象如下：
（Ⅰ）根据图象求函数解析式；
（II）由于受工厂污水处理能力的影响，环保部门要求该厂两车间任意时刻的污水排放量之和不超过5m³/h，若甲车间先投产，为满足环保要求，乙车间比甲车间至少需推迟多少小时投产？

Answer 1

分析 （Ⅰ）由图可得A，b，利用周期公式可求ω，将t=0，y=3，代入y=sin（$\frac{π}{3}$t+φ）+2，结合范围0＜φ＜π，可求φ从而可求函数解析式．
（II）设乙车间至少比甲车间推迟m小时投产，据题意得cos[$\frac{π}{3}$（t+m）]+2+cos（$\frac{π}{3}$t）+2≤5，
化简可得-$\frac{1}{2}$≤cos（$\frac{π}{6}$m）≤$\frac{1}{2}$，由m∈（0，6），可得范围2≤m≤4，即可得解．

解答 （本题满分为12分）
解：（Ⅰ）由图可得：A=$\frac{1}{2}$（3-1）=1，…1分
b=$\frac{1}{2}$（3+1）=2，…2分
∵$\frac{2π}{ω}$=6，
∴ω=$\frac{π}{3}$，…3分
∴将t=0，y=3，代入y=sin（$\frac{π}{3}$t+φ）+2，可得：sinφ=1，
又∵0＜φ＜π，
∴φ=$\frac{π}{2}$，…5分
∴y=sin（$\frac{π}{3}$t+$\frac{π}{2}$）+2=cos（$\frac{π}{3}$t）+2，
∴所求函数的解析式为y=cos（$\frac{π}{3}$t）+2，（t≥0），…6分
（注：解析式写成y=sin（$\frac{π}{3}$t+$\frac{π}{2}$）+2，或未写t≥0不扣分）
（II）设乙车间至少比甲车间推迟m小时投产，…7分
根据题意可得：cos[$\frac{π}{3}$（t+m）]+2+cos（$\frac{π}{3}$t）+2≤5，…8分
∴cos（$\frac{π}{3}$t）cos（$\frac{π}{3}$m）-sin（$\frac{π}{3}$t）sin（$\frac{π}{3}$m）+cos（$\frac{π}{3}$t）≤1，
∴[1+cos（$\frac{π}{3}$m）]cos（$\frac{π}{3}$t）-sin（$\frac{π}{3}$t）sin（$\frac{π}{3}$m）≤1，
∴$\sqrt{[1+cos（\frac{π}{3}m）]^{2}+[sin（\frac{π}{3}m）]^{2}}$≤1，
∴$\sqrt{2+2cos（\frac{π}{3}m）}$≤1，可得：2|cos（$\frac{π}{6}$m）|≤1，…11分
∴-$\frac{1}{2}$≤cos（$\frac{π}{6}$m）≤$\frac{1}{2}$，由m∈（0，6），可得：$\frac{π}{3}$≤$\frac{π}{6}$m≤$\frac{2π}{3}$，
∴2≤m≤4，
∴为满足环保要求，乙车间比甲车间至少需推迟2小时投产…12分

点评 本题主要考查了由y=Asin（ωx+φ）的部分图象确定其解析式，考查了三角函数的图象和性质，考查了计算能力和转化思想，计算量较大，属于中档题．