Question

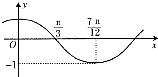
函数的图象如图所示，为了得到的图象，则只要将f（x）=cos2x的函数的图象（　　）

• A、向右平移

  π

  6

  个单位
• B、向右平移

  π

  12

  个单位
• C、向左平移

  π

  6

  个单位
• D、向左平移

  π

  12

  个单位

Answer 1

考点：函数y=Asin（ωx+φ）的图象变换

专题：三角函数的图像与性质

分析：由已知函数的图象求出函数解析式，然后利用三角函数的平移变化得到答案．

解答： 解：由图象可知，该函数的A=1，周期为4(

7π

12

-

π

3

)=π，
∴ω=2，代入(

7π

12

，-1)可得φ=

π

3

，
∴函数为f(x)=sin(2x+

π

3

)，而将函数图象向左平移

π

12

个单位长度后得到函数f(x)=sin[2(x+

π

12

)+

π

3

]=cos2x．
∴为了得到为f(x)=sin(2x+

π

3

)的图象，只要将f（x）=cos2x的函数的图象向右平移

π

12

个单位．
故选：B．

点评：本小题主要考查三角函数的性质和三角函数图象的平移，解决此类问题时，要特别注意图象左右平移的单位是相对于x说的，是中档题．