题目内容
已知tanθ=
，则
的值为（ ）
| 2 |
| 3 |
| 1+cos2θ+sin2θ |
| 1-cos2θ+sin2θ |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：原式利用二倍角的正弦、余弦函数公式化简，整理后利用同角三角函数间基本关系化简，把tanθ的值代入计算即可求出值．
解答：
解：∵tanθ=
，
∴原式=
=
=
=
．
故选：A．
| 2 |
| 3 |
∴原式=
| 1+(2cos2θ-1)+2sinθcosθ |
| 1-(1-2sin2θ)+2sinθcosθ |
| 2cosθ(cosθ+sinθ) |
| 2sinθ(cosθ+sinθ) |
| 1 |
| tanθ |
| 3 |
| 2 |
故选：A．
点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
已知函数f（x）周期为4，且当x∈（-1，3]时，f（x）=
，其中m＞0．若方程3f（x）=x恰有5个实数解，则m的取值范围为（ ）
|
A、（
| ||||||
B、（
| ||||||
C、（
| ||||||
D、（
|
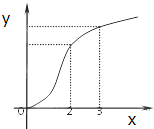
函数f（x）的图象如图所示，f′（x）是f（x）的导函数，则下列数值排序正确的是（ ）
| A、0＜f′（2）＜f′（3）＜f（3）-f（2） |
| B、0＜f′（3）＜f（3）-f（2）＜f′（3） |
| C、0＜f′（3）＜f′（2）＜f（3）-f（2） |
| D、0＜f（3）-＜f（2）＜f′（2）＜f′（3） |
已知函数f（x）=
，若方程f（x）=4有且仅有一个解，则实数a的取值范围为（ ）
|
| A、（0，3） |
| B、[0，3] |
| C、（1，4） |
| D、[1，4] |
设f（x）是定义在R上的奇函数，其f（x）=f（x-2），若f（x）在区间[2，3]单调递减，则（ ）
| A、f（x）在区间[-3，-2]单调递增 |
| B、f（x）在区间[-2，-1]单调递增 |
| C、f（x）在区间[3，4]单调递减 |
| D、f（x）在区间[1，2]单调递减 |
在△ABC中，sinA=sinC，则△ABC是（ ）
| A、直角三角形 |
| B、等腰三角形 |
| C、钝角三角形 |
| D、锐角三角形 |
下列说法正确的是（ ）
A、函数y=x+
| ||
B、函数y=sinx+
| ||
C、函数y=|x|+
| ||
D、函数y=lgx+
|
已知θ是第三象限角，且sin4θ+cos4θ=
，则sinθcosθ=（ ）
| 5 |
| 9 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|