题目内容
在△ABC中，sinA=sinC，则△ABC是（ ）
| A、直角三角形 |
| B、等腰三角形 |
| C、钝角三角形 |
| D、锐角三角形 |
考点：三角形的形状判断
专题：三角函数的求值,解三角形
分析：在△ABC中，sinA=sinC⇒A=C，从而可得答案．
解答：
解：在△ABC中，sinA=sinC，
∴A=C（或a=c），
∴△ABC是等腰三角形，
故选：B．
∴A=C（或a=c），
∴△ABC是等腰三角形，
故选：B．
点评：本题考查三角形的形状判断，着重考查正弦定理的应用，属于基础题．
练习册系列答案
相关题目
cos（α-35°）cos（α+25°）+sin（α-35°）sin（α+25°）等于（ ）
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
已知定义在[1，+∞）上的函数f（x）=
则下列结论正确的是（ ）
|
| A、函数f（x）的值域为[1，4] | ||
B、关于x的方程f（x）-
| ||
| C、当x∈[2n-1，2n]（n∈N*）时，函数f（x）的图象与x轴围成的面积为3 | ||
| D、不存在实数x0，使不等式x0f（x0）＞6成立 |
若方程x3+ax2+bx+c=0有三个不等实根x1，x2，x3则x1+x2+x3等于（ ）
| A、-a | B、-b | C、c | D、b |
已知tanθ=
，则
的值为（ ）
| 2 |
| 3 |
| 1+cos2θ+sin2θ |
| 1-cos2θ+sin2θ |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知数列1，
，
，2，
，…则3
是它的（ ）
| 2 |
| 3 |
| 5 |
| 3 |
| A、第25项 | B、第26项 |
| C、第27项 | D、第28项 |
已知函数f（x）=（2x-1）2+ax2，若不等式f（x）＜0的解集中恰有3个整数解，则（ ）
| A、f（1）f（2）＜0 |
| B、f（2）f（3）＜0 |
| C、f（3）f（4）＜0 |
| D、f（4）f（5）＜0 |
斜率为1的直线l经过抛物线y2=2x的焦点，且与抛物线相交于A、B两点，则线段AB的长是（ ）
A、2
| ||
| B、2 | ||
C、4
| ||
| D、4 |
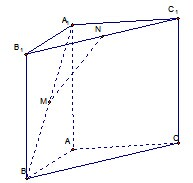如图，直三棱柱ABC-A1B1C1，∠BAC=90°，AB=AC=