题目内容
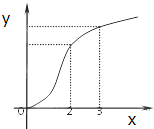
函数f(x)的图象如图所示,f′(x)是f(x)的导函数,则下列数值排序正确的是( )

| A、0<f′(2)<f′(3)<f(3)-f(2) |
| B、0<f′(3)<f(3)-f(2)<f′(3) |
| C、0<f′(3)<f′(2)<f(3)-f(2) |
| D、0<f(3)-<f(2)<f′(2)<f′(3) |
考点:函数的单调性与导数的关系
专题:导数的概念及应用
分析:由题意已知函数f(x)的图象,先判断它的单调性,然后根据函数图象斜率的变化,判断f(x)′的增减性,最后根据函数的凸凹性进行判断,从而求解.
解答:
解:由函数f(x)的图象可知:
当x≥0时,f(x)单调递增,且当x=0时,f(0)>0,
∴f′(2),f′(3),f(3)-f(2)>0,
由此可知f(x)′在(0,+∝)上恒大于0,其图象为一条直线,
∵直线的斜率逐渐减小,
∴f′(x)单调递减,
∴f′(2)>f′(3),
∵f(x)为凸函数,
∴f(3)-f(2)<f′(3)
∴0<f′(3)<f(3)-f(2)<f′(3),
故选B.
当x≥0时,f(x)单调递增,且当x=0时,f(0)>0,
∴f′(2),f′(3),f(3)-f(2)>0,
由此可知f(x)′在(0,+∝)上恒大于0,其图象为一条直线,
∵直线的斜率逐渐减小,
∴f′(x)单调递减,
∴f′(2)>f′(3),
∵f(x)为凸函数,
∴f(3)-f(2)<f′(3)
∴0<f′(3)<f(3)-f(2)<f′(3),
故选B.
点评:此题主要考查函数导数与函数单调性之间的关系,掌握并会熟练运用导数与函数单调性的关系,另外还考查学生的读图能力,要善于从图中获取信息.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
某公司租地建仓库,每月土地占用费y与仓库到车站的距离成反比,而每月库存货物费y与到车站的距离成正比,如果在距离车站10公里处建仓库,这这两项费用y和y分别为2万元和8万元,那么要使这两项费用之和最小,仓库应建在离车站( )
| A、4公里处 | B、5公里处 |
| C、3公里处 | D、2公里处 |
(2x-1)(x+2)5的展开式中含x4项的系数( )
| A、30 | B、70 | C、90 | D、150 |
sin2α等于( )
| A、2sinα |
| B、sin2α |
| C、2sinαcosα |
| D、2sin2α-1 |
已知定义在[1,+∞)上的函数f(x)=
则下列结论正确的是( )
|
| A、函数f(x)的值域为[1,4] | ||
B、关于x的方程f(x)-
| ||
| C、当x∈[2n-1,2n](n∈N*)时,函数f(x)的图象与x轴围成的面积为3 | ||
| D、不存在实数x0,使不等式x0f(x0)>6成立 |
||
|=1,|
|=2,且(
+
)•
=0,则
、
的夹角为( )
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| A、60° | B、90° |
| C、120° | D、150° |
已知tanθ=
,则
的值为( )
| 2 |
| 3 |
| 1+cos2θ+sin2θ |
| 1-cos2θ+sin2θ |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
角α(0<α<2π)的正、余弦线的长度相等,且正、余弦符号相异.那么α的值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|