题目内容
在平行六面体ABCD-A1B1C1D1中，每条棱的长都等于a，AB，AD，AA1两两夹角都是θ，求证：AC1⊥平面A1BD．
考点：直线与平面垂直的判定
专题：空间位置关系与距离
分析：证明
•
=(
+
+
)•(
-
)=0，可得
⊥
，即AC1⊥BD．同理可得：AC1⊥A1D．再利用线面垂直的判定定理即可证明．
| AC1 |
| BD |
| AA1 |
| AB |
| AD |
| AD |
| AB |
| AC1 |
| BD |
解答：
证明：如图所示，
∵
=
+
+
，
=
-
，
•
=
•
，
2=
2．
∴
•
=(
+
+
)•(
-
)
=
•
-
•
+
•
-
2+
2-
•
=0，
∴
⊥
，即AC1⊥BD．
同理可得：AC1⊥A1D．
∵A1D∩BD=D，
∴AC1⊥平面A1BD．
∵
| AC1 |
| AA1 |
| AB |
| AD |
| BD |
| AD |
| AB |
| AA1 |
| AD |
| AA1 |
| AB |
| AB |
| AD |
∴
| AC1 |
| BD |
| AA1 |
| AB |
| AD |
| AD |
| AB |
=
| AA1 |
| AD |
| AA1 |
| AB |
| AB |
| AD |
| AB |
| AD |
| AD |
| AB |
=0，
∴
| AC1 |
| BD |
同理可得：AC1⊥A1D．
∵A1D∩BD=D，
∴AC1⊥平面A1BD．
点评：本题考查了利用向量垂直与数量积的关系证明垂直、线面垂直的判定定理，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
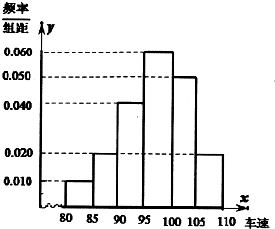2015年国庆节之前，市教育局为高三学生在紧张学习之余，不忘体能素质的提升，要求该市高三全体学生进行一套满分为120分的体能测试，市教育局为了迅速了解学生体能素质状况，按照全市高三测试学生的先后顺序，每间隔50人就抽取一人的抽样方法抽取40分进行统计分析，将这40人的体能测试成绩分成六段[80，85），[85，90），[90，95），[95，100），[100，105），[105，110）后，得到如下图的频率分布直方图．椭圆
+
=1内一点P（3，2），过点P的弦AB恰好被点P平分，则直线AB的方程为（ ）
| x2 |
| 36 |
| y2 |
| 16 |
| A、2x-3y=0 |
| B、x+y-5=0 |
| C、2x+3y-12=0 |
| D、3x-2y-5=0 |
如果圆x2+y2+Dx+Ey+F=0与x轴相切于原点，则（ ）
| A、E≠0，D=F=0 |
| B、D≠0，E≠0，F=0 |
| C、D≠0，E=F=0 |
| D、F≠0，D=E=0 |