题目内容
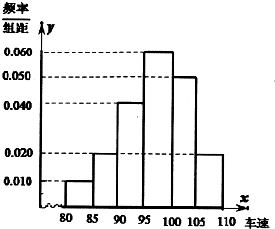 2015年国庆节之前,市教育局为高三学生在紧张学习之余,不忘体能素质的提升,要求该市高三全体学生进行一套满分为120分的体能测试,市教育局为了迅速了解学生体能素质状况,按照全市高三测试学生的先后顺序,每间隔50人就抽取一人的抽样方法抽取40分进行统计分析,将这40人的体能测试成绩分成六段[80,85),[85,90),[90,95),[95,100),[100,105),[105,110)后,得到如下图的频率分布直方图.
2015年国庆节之前,市教育局为高三学生在紧张学习之余,不忘体能素质的提升,要求该市高三全体学生进行一套满分为120分的体能测试,市教育局为了迅速了解学生体能素质状况,按照全市高三测试学生的先后顺序,每间隔50人就抽取一人的抽样方法抽取40分进行统计分析,将这40人的体能测试成绩分成六段[80,85),[85,90),[90,95),[95,100),[100,105),[105,110)后,得到如下图的频率分布直方图.(1)市教育局在采样中,用的是什么抽样方法?并估计这40人体能测试成绩平均数;
(2)从体能测试成绩在[80,90)的学生中任抽取2人,求抽出的2人体能测试成绩在[85,90)概率.
参考数据:82.5×0.01+87.5×0.02+92.5×0.04+97.5×0.06+102.5×0.05+107.5×0.02=19.4.
考点:列举法计算基本事件数及事件发生的概率,频率分布直方图
专题:概率与统计
分析:(1)根据系统抽样的特征判断抽样方法是系统抽样;根据中位数的左、右两边小矩形的面积相等求中位数;
(2)利用频数=频率×样本容量分别求得体能测试成绩在[80,85)的人数和[85,90)人数,用列举法写出从这6人中随机抽取2人的所有基本事件,找出抽出的2人中体能测试成绩在[85,90)的基本事件,利用个数比求概率..
(2)利用频数=频率×样本容量分别求得体能测试成绩在[80,85)的人数和[85,90)人数,用列举法写出从这6人中随机抽取2人的所有基本事件,找出抽出的2人中体能测试成绩在[85,90)的基本事件,利用个数比求概率..
解答:
解:(1)根据“每间隔50人就抽取一人”,符合系统抽样的原理,故市教育局在采样中,用到的是系统抽样方法.
平均数的估计值为:(82.5×0.01+87.5×0.02+92.5×0.04+97.5×0.06+102.5×0.05+107.5×0.02)×5=97.
(2)从图中可知,体能测试成绩在[80,85)的人数为0.01×5×40=2(人),分别记为m,n;
体能测试成绩在[85,90)人数为0.02×5×40=4(人),分别记为A,B,C,D,从这6人中随机抽取两人共有15种情况:mn,mA,mB,mC,mD,nA,nB,nC,nD,AB,AC,AD,BC,BD,CD共15种情况
抽出的2人中体能测试成绩在[85,90)的情况有AB,AC,AD,BC,BD,CD共6种,
故所求事件的概率P(A)=
=
.
平均数的估计值为:(82.5×0.01+87.5×0.02+92.5×0.04+97.5×0.06+102.5×0.05+107.5×0.02)×5=97.
(2)从图中可知,体能测试成绩在[80,85)的人数为0.01×5×40=2(人),分别记为m,n;
体能测试成绩在[85,90)人数为0.02×5×40=4(人),分别记为A,B,C,D,从这6人中随机抽取两人共有15种情况:mn,mA,mB,mC,mD,nA,nB,nC,nD,AB,AC,AD,BC,BD,CD共15种情况
抽出的2人中体能测试成绩在[85,90)的情况有AB,AC,AD,BC,BD,CD共6种,
故所求事件的概率P(A)=
| 6 |
| 15 |
| 2 |
| 5 |
点评:本题考查了由频率分布直方图求中位数及频数,考查了古典概型的概率计算,利用列举法求基本事件个数,是进行古典概型概率计算的常用方法.

练习册系列答案
相关题目
下列集合的表示方法正确的是( )
| A、{1,2,3,3,} |
| B、{全体有理数} |
| C、0={0} |
| D、不等式x-3>2的解集是{x|x>5} |
下面四个几何体中,左视图是四边形的几何体共有( )个.


| A、0 | B、1 | C、2 | D、3 |
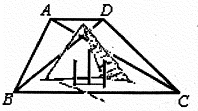 如图,在一座底部不可到达的孤山两侧,有两段平行的公路AB和CD,现测得AB=5,AC=9∠BCA=30°,∠ADB=45°
如图,在一座底部不可到达的孤山两侧,有两段平行的公路AB和CD,现测得AB=5,AC=9∠BCA=30°,∠ADB=45°