题目内容
已知正项等比数列数列{an}，bn=logaan，则数列{bn}是 （ ）
| A、等比数列 |
| B、等差数列 |
| C、既是等差数列又是等比数列 |
| D、以上都不对 |
考点：等比数列的性质
专题：计算题
分析：利用等差数列的通项公式表示出通项为an=a1•qn，求出bn-bn-1=logaq利用等差数列的定义判定出数列{bn}是等差数列．
解答：
解：设正项等比数列数列{an}的首项为a1，d；
∴an=a1•qn
bn=logaan=logaa1+nlogaq，
bn-bn-1=logaa1+nlogaq-[logaa1+（n-1）logaq]=logaq（常数）
∴数列{bn}是等差数列．
故选B
∴an=a1•qn
bn=logaan=logaa1+nlogaq，
bn-bn-1=logaa1+nlogaq-[logaa1+（n-1）logaq]=logaq（常数）
∴数列{bn}是等差数列．
故选B
点评：本题考查等差数列的通项公式及等差数列的定义，属于基础题．
练习册系列答案
相关题目
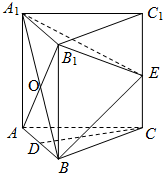如图，在三棱柱ABC-A1B1C1中，每个侧面均为正方形，D为底边AB的中点，E为侧棱CC1的中点．