题目内容
20.武汉地铁4号线每6分钟一趟列车,小明同学每天早晚两次乘地铁上学与回家,每周一至周五上五天学,如果某天至少有一次等车时间不超过2分钟,则称该天为“风顺”天(1)求小明某天恰有一次等车时间不超过2分钟的概率;
(3)记X为小明一周中“风顺”天的天数,求X的数学期望.
分析 (1)由题可知,是与区间长度有关的几何概率的求解,每隔6分钟就有一趟车经过构成全部区域,长度为10,基本事件所构成的区王等车时间不超过2分钟,长度为2,代入公式可求;
(2)可知小明一周中“风顺”天的天数X服从二项分布,然后根据二项分布的数学期望公式解之即可.
解答 解:(1)由题可知,是与区间长度有关的几何概率的求解,设每次等车时间不超过2分钟的概率为P0,
每隔6分钟就有一趟车经过构成全部区域,长度为6,
基本事件所构成的区域是小明某次等车时间不超过2分钟,长度为2,
代入公式可得P0=$\frac{2}{6}$=$\frac{1}{3}$;
某天恰有一次等车时间不超过2分钟的概率:P=${C}_{2}^{1}$×$\frac{1}{3}$×$\frac{2}{3}$=$\frac{4}{9}$;
(2)某天为“风顺”天的概率为:P2=${C}_{2}^{1}$×$\frac{1}{3}$×$\frac{2}{3}$+$\frac{1}{3}$×$\frac{1}{3}$=$\frac{5}{9}$;
依题意得,X~B(5,$\frac{5}{9}$)
∴EX=5×$\frac{5}{9}$=$\frac{25}{9}$
点评 本题主要考查了与区间长度有关的几何概率的求解,离散型随机变量的概率分布,同时考查了计算能力,属于中档题.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
10.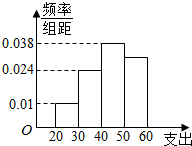 学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n且支出在[20,60)元的样本,其频率分布直方图如图所示,其中支出在[50,60)元的学生有30人,则n的值为( )
学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n且支出在[20,60)元的样本,其频率分布直方图如图所示,其中支出在[50,60)元的学生有30人,则n的值为( )
 学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n且支出在[20,60)元的样本,其频率分布直方图如图所示,其中支出在[50,60)元的学生有30人,则n的值为( )
学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n且支出在[20,60)元的样本,其频率分布直方图如图所示,其中支出在[50,60)元的学生有30人,则n的值为( )| A. | 100 | B. | 1000 | C. | 90 | D. | 900 |
11.已知集合A={x|x2<2-x},B={x|一1<x<2},则A∪B=( )
| A. | (一1,1) | B. | (一2,2) | C. | (一1,2) | D. | (一2,1) |
10.已知△ABC中,a=4,b=5,A=30°.下列对三角形解的情况的判断中,正确的是( )
| A. | 一解 | B. | 两解 | C. | 无解 | D. | 一解或无解 |
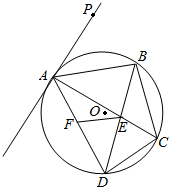 已知:如图,四边形ABCD是圆O的内接四边形,对角线AC、BD交于点E,直线AP是圆O的切线,切点为A,∠PAB=∠BAC.
已知:如图,四边形ABCD是圆O的内接四边形,对角线AC、BD交于点E,直线AP是圆O的切线,切点为A,∠PAB=∠BAC.