题目内容
8.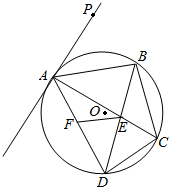 已知:如图,四边形ABCD是圆O的内接四边形,对角线AC、BD交于点E,直线AP是圆O的切线,切点为A,∠PAB=∠BAC.
已知:如图,四边形ABCD是圆O的内接四边形,对角线AC、BD交于点E,直线AP是圆O的切线,切点为A,∠PAB=∠BAC.(1)求证:AB2=BD•BE;
(2)若∠FED=∠CED,求证:点A、B、E、F四点共圆.
分析 (1)证明△ABD∽△EBA,即可证明AB2=BD•BE;
(2)证明∠BAF+∠BEF=∠BAD+∠BEF=∠FED+∠BEF=180°,即可证明点A、B、E、F四点共圆.
解答 证明:(1)∵直线AP是圆O的切线,切点为A,
∴∠PAB=∠ADB,
∴∠PAB=∠BAC,
∴∠ADB=∠BAC,
∵∠ABD=∠EBA,
∴△ABD∽△EBA,
∴$\frac{AB}{EB}$=$\frac{BD}{BA}$,
∴AB2=BD•BE;
(2)由(1)可知∠BAD=∠BEA,
∵∠BEA=∠CED,∠FED=∠CED,
∴∠BAD=∠FED,
∴∠BAF+∠BEF=∠BAD+∠BEF=∠FED+∠BEF=180°
∴点A、B、E、F四点共圆.
点评 本题考查三角形相似的证明,考查四点共圆,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
18.已知命题p:$\frac{2x}{x-1}$<1,命题q:(x+a)(x-3)<0,若p是q的充分不必要条件,则实数a的取值范围是( )
| A. | (-3,-1] | B. | [-3,-1] | C. | [1,+∞) | D. | (-∞,-3] |
3.在锐角三角形ABC中,下列结论正确的是( )
| A. | sinA>sinB | B. | cosA>cosB | C. | sinA>cosB | D. | cosA>sinB |
18.若点P(2,1)为圆(x-1)2+y2=25的弦AB的中点,则直线AB的方程为( )
| A. | x+y-3=0 | B. | 2x-y-5=0 | C. | 2x+y=0 | D. | x-y-1=0 |
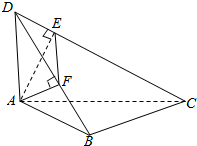 如图,在空间四边形ABCD中,DA⊥平面ABC,∠ABC=90°,AE⊥CD,AF⊥DB.
如图,在空间四边形ABCD中,DA⊥平面ABC,∠ABC=90°,AE⊥CD,AF⊥DB.