题目内容
5.在(1-2x)m的展开式中,第5项、第6项和第7项的二项式系数为等差数列,求展开式中的第2项.分析 由条件利用差数列的定义,二项式系数的性质,求得m的值,再根据二项展开式的通项公式,求得展开式中的第2项.
解答 解:由题意可得2${C}_{m}^{5}$=${C}_{m}^{4}$+${C}_{m}^{6}$,∴$\frac{2}{5(m-5)}$=$\frac{1}{(m-4)(m-5)}$+$\frac{1}{30}$,求得m=7,
故(1-2x)m的展开式中,第二项为T2=${C}_{7}^{1}$•(-2x)=-14x.
点评 本题主要考查等差数列的定义,二项式定理的应用,二项展开式的通项公式,二项式系数的性质,属于基础题.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
15.关于空间直角坐标系,下列叙述正确的是( )
| A. | P(x,y,z)中x,y,z的位置可以互换的 | |
| B. | 空间直角坐标系中的点与一个三元有序数组是一种一一对应关系 | |
| C. | 空间直角坐标系中的三条坐标轴把空间分成八个部分 | |
| D. | 某点在不同空间直角坐标系中的坐标位置可以相同 |
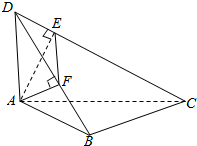 如图,在空间四边形ABCD中,DA⊥平面ABC,∠ABC=90°,AE⊥CD,AF⊥DB.
如图,在空间四边形ABCD中,DA⊥平面ABC,∠ABC=90°,AE⊥CD,AF⊥DB.