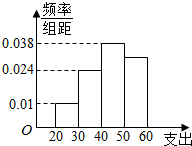学校为了调查学生在课外读物方面的支出情况.抽出了一个容量为n且支出在[20.60)元的样本.其频率分布直方图如图所示.其中支出在[50.60)元的学生有30人.则n的值为( )A．100B．1000C．90D．900 题目和参考答案——青夏教育精英家教网—

题目内容

10．

学校为了调查学生在课外读物方面的支出情况，抽出了一个容量为n且支出在[20，60）元的样本，其频率分布直方图如图所示，其中支出在[50，60）元的学生有30人，则n的值为（　　）

A．

100

B．

1000

C．

D．

900

分析根据频率直方图的意义，由前三个小组的频率可得样本在[50，60）元的频率，计算可得样本容量．

解答解：由题意可知：前三个小组的频率之和=（0.01+0.024+0.036）×10=0.7，
∴支出在[50，60）元的频率为1-0.7=0.3，
∴n的值=$\frac{30}{0.3}$=100；
故选：A．

点评本题是对频率、频数灵活运用的综合考查，各小组频数之和等于数据总和，各小组频率之和等于1．

练习册系列答案

小考必备小升初三年真题测试卷系列答案

宏翔文化全国名校中考模拟试题系列答案

三点一测学霸必刷题系列答案

名榜文化假期作业寒假郑州大学出版社系列答案

相关题目

20．函数y=$\frac{1}{x-1}+1$的图象是下列图象中的（　　）

1．已知集合M={x|x≥1}，N={x|x²≤4}，则∁_R（M∩N）=（　　）

18．已知命题p：$\frac{2x}{x-1}$＜1，命题q：（x+a）（x-3）＜0，若p是q的充分不必要条件，则实数a的取值范围是（　　）

5．已知向量$\overrightarrow{a}$=（1，2），$\overrightarrow{a}$⊥$\overrightarrow{b}$，则$\overrightarrow{b}$可以为（　　）

15．已知直线y=kx+3与圆（x-2）²+（y-3）²=4相交于M，N两点，点$|MN|≥2\sqrt{3}$，求k的取值范围．

2．函数f（x）在[a，b]上有定义，若对任意x₁，x₂∈[a，b]，有f（$\frac{{x}_{1}+{x}_{2}}{2}$）≤$\frac{1}{2}$[f（x₁）+f（x₂）]，则称f（x）在[a，b]上具有性质P．设f（x）在[1，3]上具有性质P，现给出如下题：
①f（x）在[1，3]上的图象时连续不断的
②f（x）在[1，$\sqrt{3}$]上具有性质P
③若f（x）在x=2处取得最大值1，则f（x）=1，x∈[1，3]
④对任意x₁，x₂，x₃，x₄∈[1，3]，有f（$\frac{{x}_{1}+{x}_{2}+{x}_{3}+{x}_{4}}{4}$）≤$\frac{1}{4}$[f（x₁）+f（x₂）+f（x₃）+f（x₄）]
其中真命题的序号③④．

19．已知a为常数，若曲线y=ax²+3x-lnx存在与直线x+y-1=0垂直的切线，则实数a的取值范围是[-$\frac{1}{2}$，+∞）．

20．武汉地铁4号线每6分钟一趟列车，小明同学每天早晚两次乘地铁上学与回家，每周一至周五上五天学，如果某天至少有一次等车时间不超过2分钟，则称该天为“风顺”天
（1）求小明某天恰有一次等车时间不超过2分钟的概率；
（3）记X为小明一周中“风顺”天的天数，求X的数学期望．

试题分类