题目内容
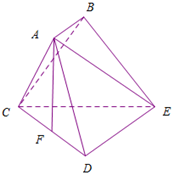 如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为的中点.
如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为的中点.(1)求证:AF⊥平面CDE;
(2)求异面直线CB与AE所成角的大小;?求平面ACD和平面BCE所成锐二面角的大小.
考点:二面角的平面角及求法,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)由已知得DE⊥AF,AF⊥CD,由此能证明AF⊥平面CDE.
(2)取CE的中点Q,连结FQ,由FD,FQ,FA两两垂直,建立空间直角坐标系,利用向量法能求出异面直线CB与AE所成角的大小和平面ACD和平面BCE所成锐二面角的大小.
(2)取CE的中点Q,连结FQ,由FD,FQ,FA两两垂直,建立空间直角坐标系,利用向量法能求出异面直线CB与AE所成角的大小和平面ACD和平面BCE所成锐二面角的大小.
解答:
(1)证明:∵DE⊥平面ACD,AF?平面ACD,
∴DE⊥AF,又∵AC=AD,F为CD中点,
∴AF⊥CD,
∵CD∩DE=D,
∴AF⊥平面CDE.
(2)解:取CE的中点Q,连结FQ,
∵F为CD的中点,故DE⊥平面ACD,
∴FQ⊥平面ACD,由(1)知FD,FQ,FA两两垂直,
故建立如图所示的空间直角坐标系,
则F(0,0,0),C(-1,0,0),
A(0,0,
),B(0,1,
),E(1,2,0),
=(1,1,
),
=(1,2,-
),
∵
•
=0,∴异面直线CB与AE所成角的大小为90°.
=(1,1,
),
=(2,2,0),
设平面BCE的法向量
=(x,y,z),
则
,
取x=1,得
=(1,-1,0),
又平面ACD的一个法向量为
=(0,1,0),
∴|cos<
,
>|=|
|=
,
∴平面ACD和平面BCE所成锐二面角的大小为45°.

∴DE⊥AF,又∵AC=AD,F为CD中点,
∴AF⊥CD,
∵CD∩DE=D,
∴AF⊥平面CDE.
(2)解:取CE的中点Q,连结FQ,
∵F为CD的中点,故DE⊥平面ACD,
∴FQ⊥平面ACD,由(1)知FD,FQ,FA两两垂直,
故建立如图所示的空间直角坐标系,
则F(0,0,0),C(-1,0,0),
A(0,0,
| 3 |
| 3 |
| CB |
| 3 |
| AE |
| 3 |
∵
| CB |
| AE |
| CB |
| 3 |
| CE |
设平面BCE的法向量
| n |
则
|
取x=1,得
| n |
又平面ACD的一个法向量为
| FQ |
∴|cos<
| FQ |
| n |
| 0-1+0 | ||
|
| ||
| 2 |
∴平面ACD和平面BCE所成锐二面角的大小为45°.
点评:本题考查直线与平面垂直的证明,考查异面直线CB与AE所成角的大小和平面ACD和平面BCE所成锐二面角的大小的求法,解题时要注意向量法的合理运用.

练习册系列答案
相关题目
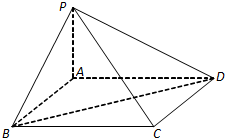 如图,在四棱锥P-ABCD中,底面ABCD是菱形,且PB=PD.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,且PB=PD.