题目内容
已知椭圆C:4x2+y2=1及直线l:y=x+m,m∈R.
(1)当m为何值时,直线l与椭圆C有公共点?
(2)若直线l被椭圆C截得的弦长为
,求直线l的方程.
(1)当m为何值时,直线l与椭圆C有公共点?
(2)若直线l被椭圆C截得的弦长为
2
| ||
| 5 |
考点:直线与圆锥曲线的关系,椭圆的标准方程
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:(1)将直线的方程y=x+m与椭圆的方程4x2+y2=1联立,得到5x2+2mx+m2-1=0,利用△=-16m2+20≥0即可求得m的取值范围;
(2)联立直线方程和椭圆方程,消去y,得到x的方程,运用韦达定理和判别式大于0,再由弦长公式,解得m,即可得到直线方程.
(2)联立直线方程和椭圆方程,消去y,得到x的方程,运用韦达定理和判别式大于0,再由弦长公式,解得m,即可得到直线方程.
解答:
解:(1)把直线y=x+m代入椭圆方程得:4x2+(x+m)2=1,
即:5x2+2mx+m2-1=0,
△=(2m)2-4×5×(m2-1)=-16m2+20≥0
解得:-
≤m≤
;
(2)设该直线与椭圆相交于两点A(x1,y1),B(x2,y2),
则x1,x2是方程5x2+2mx+m2-1=0的两根,由韦达定理可得:
x1+x2=-
,x1x2=
,
|AB|=
|x1-x2|=
•
=
•
=
,解得,m=±1.检验成立.
则所求直线的方程是:y=x+1或y=x-1.
即:5x2+2mx+m2-1=0,
△=(2m)2-4×5×(m2-1)=-16m2+20≥0
解得:-
| ||
| 2 |
| ||
| 2 |
(2)设该直线与椭圆相交于两点A(x1,y1),B(x2,y2),
则x1,x2是方程5x2+2mx+m2-1=0的两根,由韦达定理可得:
x1+x2=-
| 2m |
| 5 |
| m2-1 |
| 5 |
|AB|=
| 1+k2 |
| 1+k2 |
| (x1+x2)2-4x1x2 |
| 1+1 |
(-
|
=
2
| ||
| 5 |
则所求直线的方程是:y=x+1或y=x-1.
点评:本题考查直线与圆锥曲线的位置关系与弦长问题,难点在于弦长公式的灵活应用,属于中档题.

练习册系列答案
相关题目
有矩阵A3×2,B2×3,C3×3,下列运算可行的是( )
| A、AC | B、BAC |
| C、ABC | D、AB-AC |
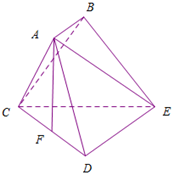 如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为的中点.
如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为的中点.