题目内容
用行列式讨论关于x,y的二元一次方程组
的解的情况,并说明各自的几何意义.
|
考点:逆矩阵与二元一次方程组
专题:矩阵和变换
分析:首先,分情况当m≠±2、m=-2、m=2三种情形进行讨论,几何意义:分m≠±2、m=-2、m=2三种情形说明.
解答:
解:D=
=(m-2)(m+2),Dx=
=m(m-2),Dy=
=(m-2)(m+1)
(1)当m≠±2时,D≠0方程组有唯一解,此时
,即
;
(2)当m=2时,D=Dx=Dy=0,方程组有无穷多组解,通解可表示为
(t∈R),
(3)当m=-2时,D=0,Dx≠0,Dy≠0,此时方程组无解.
几何意义:设l1:mx+4y=m+2,l2:x+my=m
当m≠±2时,方程组唯一解,则直线l1与l2相交;
当m=-2时,方程组无解,则直线l1与l2平行;
当m=2时,方程组无穷多解,则直线l1与l2重合.
|
|
|
(1)当m≠±2时,D≠0方程组有唯一解,此时
|
|
(2)当m=2时,D=Dx=Dy=0,方程组有无穷多组解,通解可表示为
|
(3)当m=-2时,D=0,Dx≠0,Dy≠0,此时方程组无解.
几何意义:设l1:mx+4y=m+2,l2:x+my=m
当m≠±2时,方程组唯一解,则直线l1与l2相交;
当m=-2时,方程组无解,则直线l1与l2平行;
当m=2时,方程组无穷多解,则直线l1与l2重合.
点评:本题重点考查了方程组与行列式之间的关系,分类讨论思想及其应用等知识,属于中档题.解题关键是分类中如何划分“类”.

练习册系列答案
相关题目
64
-(-
)0+log28的值为( )
| 1 |
| 3 |
| 2 |
| 3 |
| A、0 | B、1 | C、3 | D、6 |
经过空间一点P作与直线a成90°角的直线有( )
| A、0条 | B、1条 |
| C、有限条 | D、无数条 |
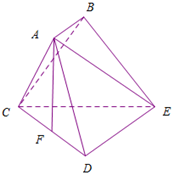 如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为的中点.
如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为的中点.