题目内容
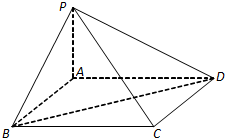如图，在四棱锥P-ABCD中，底面ABCD是菱形，且PB=PD．（1）求证：BD⊥PC；
（2）若平面PBC与平面PAD的交线为l，求证：BC∥l．
考点：直线与平面平行的性质
专题：空间位置关系与距离
分析：（1）根据线面垂直的性质证明BD⊥平面PAC即可．
（2）根据线面平行的性质定理证明BC∥平面PAD即可．
（2）根据线面平行的性质定理证明BC∥平面PAD即可．
解答：
解：（1）设AC与BD的中点为O，连结PO，
∵PB=PD，∴PO⊥BD，
∵底面ABCD是菱形，∴BD⊥AC，
∵PO∩AC=0，
∴BD⊥平面PAC，
∵PC?平面PAC，
∴BD⊥PC．
（2）∵BC∥AD，BC?面PAD，AD?面PAD，
∴BC∥面PAD．
∵平面PBC与平面PAD的交线为l，
∴BC∥l．
∵PB=PD，∴PO⊥BD，
∵底面ABCD是菱形，∴BD⊥AC，
∵PO∩AC=0，
∴BD⊥平面PAC，
∵PC?平面PAC，
∴BD⊥PC．
（2）∵BC∥AD，BC?面PAD，AD?面PAD，
∴BC∥面PAD．
∵平面PBC与平面PAD的交线为l，
∴BC∥l．
点评：本题主要考查空间直线和平面垂直的性质以及线面平行的性质的应用，要求熟练掌握相应的定理．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
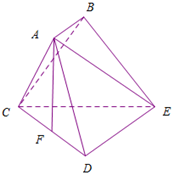如图，已知多面体ABCDE中，AB⊥平面ACD，DE⊥平面ACD，AC=AD=CD=DE=2，AB=1，F为的中点．有矩阵A3×2，B2×3，C3×3，下列运算可行的是（ ）
| A、AC | B、BAC |
| C、ABC | D、AB-AC |