题目内容
2.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的离心率为$\frac{1}{2}$,两个焦点恰好在圆O:x2+y2=1上,若过椭圆C左焦点F的直线l与圆O的另一个交点为G,线段FG的中点为M,直线MO交椭圆C于A,B两点,且|AB|=$2\sqrt{2}$|FG|,求直线l的方程.分析 由题意可得:c=1,$\frac{c}{a}=\frac{1}{2}$,a2=b2+c2,联立解出可得:椭圆C的方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1.设直线AB的方程为:y=kx(k≠0),由FG⊥AB,F(-1,0),可得直线FG的方程为:y=-$\frac{1}{k}$(x+1),即x+ky+1=0.
圆心O到直线FG的距离d=$\frac{1}{\sqrt{1+{k}^{2}}}$,|FG|=2$\sqrt{1-{d}^{2}}$,联立$\left\{\begin{array}{l}{y=kx}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,解得x2,y2,可得|AB|2=4(x2+y2),利用∵|AB|=$2\sqrt{2}$|FG|,解出k即可得出.
解答 解:由题意可得:c=1,$\frac{c}{a}=\frac{1}{2}$,a2=b2+c2,
联立解得a=2,b2=3.
∴椭圆C的方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1.设直线AB的方程为:y=kx(k≠0),
∵FG⊥AB,F(-1,0),∴直线FG的方程为:y=-$\frac{1}{k}$(x+1),即x+ky+1=0.
圆心O到直线FG的距离d=$\frac{1}{\sqrt{1+{k}^{2}}}$,∴|FG|=2$\sqrt{1-{d}^{2}}$=$\frac{2|k|}{\sqrt{1+{k}^{2}}}$,
联立$\left\{\begin{array}{l}{y=kx}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,解得x2=$\frac{12}{3+4{k}^{2}}$,y2=$\frac{12{k}^{2}}{3+4{k}^{2}}$.
∴|AB|2=4(x2+y2)=$\frac{48(1+{k}^{2})}{3+4{k}^{2}}$,
∵|AB|=$2\sqrt{2}$|FG|,∴$\frac{48(1+{k}^{2})}{3+4{k}^{2}}$=$\frac{8×4{k}^{2}}{1+{k}^{2}}$,
解得k=±$\root{4}{\frac{3}{5}}$.
∴直线l的方程为$±\root{4}{\frac{3}{5}}$y+x+1=0.
点评 本题考查了椭圆与圆的标准方程及其性质、直线与椭圆及其圆相交弦长问题、点到直线的距离公式,考查了推理能力与计算能力,属于难题.

| A. | 5 | B. | 4.5 | C. | 3.5 | D. | 不能确定 |
| A. | 0 | B. | -1或0 | C. | 0或1 | D. | 0或1或3 |

| A. | 80+16$\sqrt{2}$+16$\sqrt{3}$ | B. | 80+12$\sqrt{2}$+16$\sqrt{3}$ | C. | 80+16$\sqrt{2}$+12$\sqrt{3}$ | D. | 80+12$\sqrt{2}$+12$\sqrt{3}$ |
| A. | $\frac{1}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{5}{14}$ | D. | $\frac{4}{7}$ |
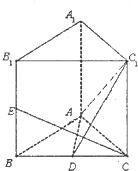 如图在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AC=2$\sqrt{2}$,BC=BB1=4,D、E分别为BC,BB1的中点.
如图在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AC=2$\sqrt{2}$,BC=BB1=4,D、E分别为BC,BB1的中点.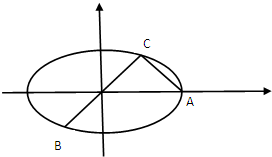 如图,已知A,B,C是长轴为4的椭圆E上的三点,点A是长轴的
如图,已知A,B,C是长轴为4的椭圆E上的三点,点A是长轴的