题目内容
6.设随机变量X的概率分布表如下:| X | 1 | 2 | 3 | 4 |
| P | $\frac{1}{4}$ | a | $\frac{3}{8}$ | b |
分析 由离散型随机变量的分布列的性质和数学期望的性质,列出方程组求出a,b,由此能求出结果.
解答 解:∵E(X)=2.5,
∴由随机变量X的概率分布表,得:
$\left\{\begin{array}{l}{\frac{1}{4}+a+\frac{3}{8}+b=1}\\{1×\frac{1}{4}+2a+3×\frac{3}{8}+4b=2.5}\end{array}\right.$,
解得a=$\frac{3}{16}$,b=$\frac{3}{16}$.
∴a-b=$\frac{3}{16}-\frac{3}{16}$=0.
故答案为:0.
点评 本题考查概率之差的求法,是基础题,解题时要认真审题,注意离散型随机变量的分布列、数学期望的性质的合理运用.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
1.对任意实数a,b定义运算“⊙”:a⊙b=$\left\{\begin{array}{l}a,a-b≤1\\ b,a-b>1\end{array}$设f(x)=2x+1⊙(1-x),若函数f(x)与函数g(x)=x2-6x在区间(m,m+1)上均为减函数,且m∈{-1,0,1,3},则m的值为( )
| A. | 0 | B. | -1或0 | C. | 0或1 | D. | 0或1或3 |
1.从区间[-2,9]中任取一个实数a,则恰使得函数f(x)=ln(ax2-2x+a)存在最大值或最小值的概率为( )
| A. | $\frac{1}{11}$ | B. | $\frac{8}{11}$ | C. | $\frac{9}{11}$ | D. | $\frac{10}{11}$ |
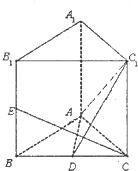 如图在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AC=2$\sqrt{2}$,BC=BB1=4,D、E分别为BC,BB1的中点.
如图在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AC=2$\sqrt{2}$,BC=BB1=4,D、E分别为BC,BB1的中点.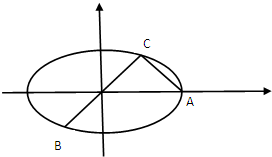 如图,已知A,B,C是长轴为4的椭圆E上的三点,点A是长轴的
如图,已知A,B,C是长轴为4的椭圆E上的三点,点A是长轴的