题目内容
19.某中学为了解初三年级学生“掷实心球”项目的整体情况,随机抽取男、女生各20名进行测试,记录的数据如下: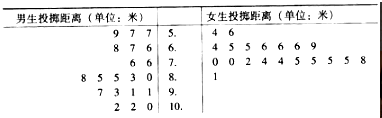
已知该项目评分标准为:
| 男生投掷距离(米) | … | [5.4,6.0) | [6.0,6.6) | [6.6,7.4) | [7.4,7.8) | [7.8,8.6) | [8.6,10.0) | [10.0,+∞) |
| 女生投掷距离(米) | … | [5.1,5.4) | [5.4,5.6) | [5.6,6.4) | [6.4,6.8) | [6.8,7.2) | [7.2,7.6) | [7.6,+∞) |
| 个人得分(分) | … | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
(Ⅰ)求上述20名女生得分的中位数和众数;
(Ⅱ)从上述20名男生中,随机抽取2名,求抽取的2名男生中优秀人数X的分布列;
(Ⅲ)根据以上样本数据和你所学的统计知识,试估计该年级学生实心球项目的整体情况.(写出两个结论即可)
分析 (Ⅰ)由茎叶图能求出20名女生掷实心球得分的中位数和众数.
(Ⅱ)X的可能取值为0,1,2,分别求出相应的概率,由此能坟出抽取的2名男生中优秀人数X的分布列.
(Ⅲ)由茎叶图得20名男生和女生掷实心球得分的中位数、众数、平均数,由此能求出结果.
解答 (共13分)
解:(Ⅰ)20名女生掷实心球得分如下:
5,6,7,7,7,7,7,7,8,8,8,9,9,9,9,9,9,9,10,10.
所以中位数为8,众数为9. …(3分)
(Ⅱ)X的可能取值为0,1,2.…(4分)
$P({X=0})=\frac{{C_{12}^2}}{{C_{20}^2}}=\frac{33}{95}$,
$P({X=1})=\frac{{C_{12}^1C_8^1}}{{C_{20}^2}}=\frac{48}{95}$,
$P({X=2})=\frac{C_8^2}{{C_{20}^2}}=\frac{14}{95}$,
所以抽取的2名男生中优秀人数X的分布列为:
| X | 0 | 1 | 2 |
| P | $\frac{33}{95}$ | $\frac{48}{95}$ | $\frac{14}{95}$ |
(Ⅲ)由茎叶图得20名男生掷实心球得分如下:
4,4,4,6,6,6,7,7,8,8,8,8,9,9,9,9,9,10,10,10.
所以中位数为8,众数为9.
20名女生掷实心球得分的平均数为:$\overline{{x}_{女}}$=$\frac{1}{20}$(5+6+7+7+7+7+7+7+8+8+8+9+9+9+9+9+9+9+10+10)=8,
20名男生掷实心球得分的平均数为:$\overline{{x}_{男}}$=$\frac{1}{20}$(4+4+4+6+6+6+7+7+8+8+8+8+9+9+9+9+9+10+10+10)=7.55.
∴该年级学生实心球项目的整体情况为:
①男生和女生的得分的中位数和众数相等;
②男生得分的平均数小于女生得分的平均数. …(13分)
评分建议:从平均数、方差、极差、中位数、众数等角度对整个年级学生掷实心球项目的情况进行合理的说明即可;也可以对整个年级男、女生该项目情况进行对比;或根据目前情况对学生今后在该项目的训练提出合理建议.
点评 本题考查中位数、众数、离散型随机变量的分布列的求法,是中档题,解题时要认真审题,注意茎叶图的性质的合理运用.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
7.如图是某几何体的三视图,则该几何体的表面积为( )


| A. | 80+16$\sqrt{2}$+16$\sqrt{3}$ | B. | 80+12$\sqrt{2}$+16$\sqrt{3}$ | C. | 80+16$\sqrt{2}$+12$\sqrt{3}$ | D. | 80+12$\sqrt{2}$+12$\sqrt{3}$ |
4.一袋中装有分别标记着1,2,3数字的3个小球,每次从袋中取出一个球(每只小球被取到的可能性相同),现连续取2次球,若每次取出一个球后放回袋中,记2次取出的球中标号最小的数字与最大的数字分别为X,Y,设ξ=Y-X,则Eξ=( )
| A. | $\frac{4}{9}$ | B. | $\frac{2}{3}$ | C. | $\frac{8}{9}$ | D. | 1 |
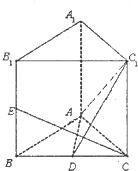 如图在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AC=2$\sqrt{2}$,BC=BB1=4,D、E分别为BC,BB1的中点.
如图在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AC=2$\sqrt{2}$,BC=BB1=4,D、E分别为BC,BB1的中点.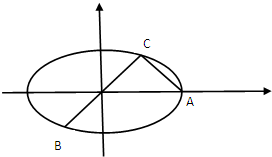 如图,已知A,B,C是长轴为4的椭圆E上的三点,点A是长轴的
如图,已知A,B,C是长轴为4的椭圆E上的三点,点A是长轴的 如图,在三棱锥A-BCD中,AB⊥平面BCD,AC=AD=2,BC=BD=1,点E是线段AD的中点.
如图,在三棱锥A-BCD中,AB⊥平面BCD,AC=AD=2,BC=BD=1,点E是线段AD的中点.