题目内容
某寻呼台共有客户3000人,若寻呼台准备了100份小礼品,邀请客户在指定时间来领取.假设任一客户去领奖的概率为4%.问:寻呼台能否向每一位顾客都发出奖品邀请?若能使每一位领奖人都得到礼品,寻呼台至少应准备多少礼品?
考点:概率的意义
专题:概率与统计
分析:根据题意来领奖的人数服从二项分布,然后求其期望就可以了.
解答:
解:设来领奖的人数ξ=k(0,1,2,3,…3000),
所以p(ξ=k)=
(0.04)k(1-0.04)3000-k,
可见ξ~B(3000,0.04),
所以,Eξ=3000×0.04=120(人)>100(人).
答:不能,寻呼台至少应准备120份礼品.
所以p(ξ=k)=
| ∁ | k 3000 |
可见ξ~B(3000,0.04),
所以,Eξ=3000×0.04=120(人)>100(人).
答:不能,寻呼台至少应准备120份礼品.
点评:本题主要考查随机变量的二次分布和期望,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知全集U=R,集合A={x|x2-2x≤0},集合B={y|y=ex,x∈R},那么(∁UA)∩B=( )
| A、{x|x>2} |
| B、{x|x<0} |
| C、{x|0<x≤1} |
| D、{x|1<x≤2} |
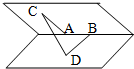 如图在一个二面角的棱上有两个点A,B,线段AC,BD分别在这个二面角的两个面内,并且都垂直于棱AB,AB=4cm,AC=6cm,BD=8cm,CD=2
如图在一个二面角的棱上有两个点A,B,线段AC,BD分别在这个二面角的两个面内,并且都垂直于棱AB,AB=4cm,AC=6cm,BD=8cm,CD=2