题目内容
在△ABC中,角A,B,C的对边分别为a,b,c,且满足(2c-b)cosA=acosB.
(Ⅰ)求角A的大小;
(Ⅱ)若a=4,求△ABC的面积的最大值.
(Ⅰ)求角A的大小;
(Ⅱ)若a=4,求△ABC的面积的最大值.
考点:余弦定理,正弦定理
专题:解三角形
分析:(1)由正弦定理和三角函数公式可得cosA=
,可得A=
;
(2)由余弦定理结合基本不等式可得16=b2+c2-bc≥2bdc-bc,可得bc的最大值为16,进而可得△ABC的面积的最大值.
| 1 |
| 2 |
| π |
| 3 |
(2)由余弦定理结合基本不等式可得16=b2+c2-bc≥2bdc-bc,可得bc的最大值为16,进而可得△ABC的面积的最大值.
解答:
解:(1)∵(2c-b)cosA=acosB,
∴由正弦定理可得(2sinA-sinB)cosA=sinAcosB,
变形可得2sinCcosA=sinBcosA+sinAcosB=sin(A+B)=sinC,
∵C为三角形的内角,sinC≠0,∴cosA=
,A=
;
(2)由余弦定理可得a2=b2+c2-2bccosA,
代入数据可得16=b2+c2-bc≥2bdc-bc,∴bc≤16
当且仅当b=c时取等号,
∴△ABC的面积S=
bcsinA=
bc≤4
,
当且仅当b=c时取等号,
∴△ABC的面积的最大值为4
∴由正弦定理可得(2sinA-sinB)cosA=sinAcosB,
变形可得2sinCcosA=sinBcosA+sinAcosB=sin(A+B)=sinC,
∵C为三角形的内角,sinC≠0,∴cosA=
| 1 |
| 2 |
| π |
| 3 |
(2)由余弦定理可得a2=b2+c2-2bccosA,
代入数据可得16=b2+c2-bc≥2bdc-bc,∴bc≤16
当且仅当b=c时取等号,
∴△ABC的面积S=
| 1 |
| 2 |
| ||
| 4 |
| 3 |
当且仅当b=c时取等号,
∴△ABC的面积的最大值为4
| 3 |
点评:本题考查正余弦定理,涉及基本不等式求最值,属比较基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数f(x)的定义域为{x|x≠0},f(x)>0.满足f(x•y)=f(x)•f(y),且在区间(0,+∞)上单调递增,若实数a满足f(log2a)+f(log
a)≤2f(1),则a的取值范围是( )
| 1 |
| 2 |
| A、[1,2] | ||
B、(0,
| ||
C、[
| ||
| D、(0,1)∪(1,2] |
函数f(x)的定义域为R,f(-2)=2013,对任意x∈R都有f′(x)<2x成立,则不等式f(x)<x2+2009的解集是( )
| A、(-2,2) |
| B、(-2,+∞) |
| C、(-∞,-2) |
| D、(-∞,+∞) |
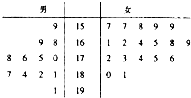 某县职工运动会将在本县一中运动场隆重召开,为了搞好接待工作,执委会在一中招募了12名男性志愿者和18名女性志愿者,调查发现,这30名志愿者的身高如图:(单位:cm)
某县职工运动会将在本县一中运动场隆重召开,为了搞好接待工作,执委会在一中招募了12名男性志愿者和18名女性志愿者,调查发现,这30名志愿者的身高如图:(单位:cm)