题目内容
已知△ABC内部的一点O，恰使
+2
+3
=
，则△OAB，△OAC，△OBC的面积之比为 ．（结果须化为最简）
| OA |
| OB |
| OC |
| 0 |
考点：三角形的面积公式
专题：解三角形,平面向量及应用
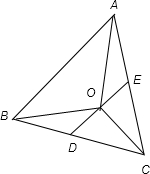
分析：如图所示，由
+2
+3
=
，可得
+
+2(
+
)=
，如图D，E分别是对应边的中点，由平行四边形法则知：
+2
=
，O为三角形ABC中位线DE的三等分点（靠近D），即可得出S△OAB=
S△ABC，S△OBC=
S△ABC，S△OAC=
S△ABC．
| OA |
| OB |
| OC |
| 0 |
| OA |
| OC |
| OB |
| OC |
| 0 |
| OE |
| OD |
| 0 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 3 |
解答：
解：∵
+2
+3
=
，
∴
+
+2(
+
)=
，
如图D，E分别是对应边的中点，
由平行四边形法则知：
+2
=
，
∴O为三角形ABC中位线DE的三等分点（靠近D）
∴S△OAB=
S△ABC，S△OBC=
S△ABC，S△OAC=
S△ABC，
∴△OAB，△OAC，△OBC的面积之比=
：
：
=3：2：1．
故答案为：3：2：1．
解：∵| OA |
| OB |
| OC |
| 0 |
∴
| OA |
| OC |
| OB |
| OC |
| 0 |
如图D，E分别是对应边的中点，
由平行四边形法则知：
| OE |
| OD |
| 0 |
∴O为三角形ABC中位线DE的三等分点（靠近D）
∴S△OAB=
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 3 |
∴△OAB，△OAC，△OBC的面积之比=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
故答案为：3：2：1．
点评：本题考查了向量的平行四边形法则、三角形的面积之比，考查了作图的能力，考查了推理能力与计算能力，属于难题．
练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
一卷搞定系列答案
名校作业本系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
在如图所示的几何体中，四边形ABCD是直角梯形，AD∥BC，AB⊥BC，AD=2，AB=3，BC=BE=7，△DCE是边长为6的正三角形．已知y=f（x）+x2是奇函数，且f（1）=1，若g（x）=f（x）+2，则g（-1）=（ ）
| A、-1 | B、0 | C、1 | D、2 |