题目内容
三棱锥A-BCD及其侧视图、俯视图如图所示,设M,N分别为线段AD,AB的中点,P为线段BC上的点,且MN⊥NP.

(1)证明:P是线段BC的中点;
(2)求二面角A-NP-M的余弦值.

(1)证明:P是线段BC的中点;
(2)求二面角A-NP-M的余弦值.
考点:二面角的平面角及求法,直线与平面平行的判定,用空间向量求平面间的夹角
专题:空间向量及应用
分析:(1)用线面垂直的性质和反证法推出结论,
(2)先建空间直角坐标系,再求平面的法向量,即可求出二面角A-NP-M的余弦值.
(2)先建空间直角坐标系,再求平面的法向量,即可求出二面角A-NP-M的余弦值.
解答:
解:(1)由三棱锥A-BCD及其侧视图、俯视图可知,在三棱锥A-BCD中:
平面ABD⊥平面CBD,AB=AD=BD=CD=CB=2
设O为BD的中点,连接OA,OC
于是OA⊥BD,OC⊥BD 所以BD⊥平面OAC⇒BD⊥AC
因为M,N分别为线段AD,AB的中点,所以MN∥BD,MN⊥NP,故BD⊥NP
假设P不是线段BC的中点,则直线NP与直线AC是平面ABC内相交直线
从而BD⊥平面ABC,这与∠DBC=60°矛盾,所以P为线段BC的中点
(2)以O为坐标原点,OB,OC,OA分别为x,y,z轴建立空间直角坐标系,
则A(0,0,
),M(-
,O,-
),N(
,0,
),P(
,
,0)
于是
=(
,0,
),
=(0,
,
),
=(1,0,0)
设平面ANP和平面NPM的法向量分别为
=(x1,y1,z1)和
=(x2,y2,z2)
由
,则
,设z1=1,则
=(
,1,1)
由
,则
,设z2=1,则
=(0,1,1)
cos<
,
>=
=
=
所以二面角A-NP-M的余弦值
平面ABD⊥平面CBD,AB=AD=BD=CD=CB=2
设O为BD的中点,连接OA,OC
于是OA⊥BD,OC⊥BD 所以BD⊥平面OAC⇒BD⊥AC
因为M,N分别为线段AD,AB的中点,所以MN∥BD,MN⊥NP,故BD⊥NP
假设P不是线段BC的中点,则直线NP与直线AC是平面ABC内相交直线
从而BD⊥平面ABC,这与∠DBC=60°矛盾,所以P为线段BC的中点
(2)以O为坐标原点,OB,OC,OA分别为x,y,z轴建立空间直角坐标系,
则A(0,0,
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
于是
| AN |
| 1 |
| 2 |
| ||
| 2 |
| PN |
| ||
| 2 |
| ||
| 2 |
| MN |
设平面ANP和平面NPM的法向量分别为
| m |
| n |
由
|
|
| m |
| 3 |
由
|
|
| n |
cos<
| m |
| n |
| ||||
|
|
| 2 | ||||
|
| ||
| 5 |
所以二面角A-NP-M的余弦值
| ||
| 5 |
点评:本题考查线线的位置关系,考查二面角知识的应用,解题的关键是掌握用向量的方法求二面角大小的步骤,属于中档题.

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
 某几何体的三视图(单位:cm)如图所示,则该几何体最长的一条侧棱长度是( )
某几何体的三视图(单位:cm)如图所示,则该几何体最长的一条侧棱长度是( )| A、5cm | ||
B、
| ||
C、
| ||
D、
|
首项为1,公差不为0的等差数列{an}中,a3、a4、a6是一个等比数列的前三项,则这个等比数列的第四项是( )
| A、8 | B、-8 | C、-6 | D、不确定 |
已知集合A={y丨y=x2},B={x丨
<0},求A∩B=( )
| x+1 |
| x-2 |
| A、[0,+∞) |
| B、(-1,2) |
| C、[0,2) |
| D、(-1,0] |
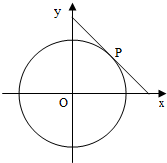 圆x2+y2=4的切线与x轴正半轴,y轴正半轴围成一个三角形,当该三角形面积最小时,切点为P(如图).
圆x2+y2=4的切线与x轴正半轴,y轴正半轴围成一个三角形,当该三角形面积最小时,切点为P(如图).