题目内容
设Q是半径为1的圆上一动点,若MN是该圆的一条动弦,且|MN|=
,则
•
的取值范围是 、
| 2 |
| MQ |
| MN |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:以与MN平行且过圆心的直线为x轴,以MN的垂直平分线为y轴,表示出M,N 点的坐标,设出Q点的坐标((cosθ,sinθ)),表示出
•
,根据cosθ的范围,问题得以解决.
| MQ |
| MN |
解答:
解:以与MN平行且过圆心的直线为x轴,以MN的垂直平分线为y轴,
∵|MN|=
∴M(-
,
),N(
,
),
设Q(cosθ,sinθ)
则
=(cosθ+
,sinθ-
),
=(
,0),
∴
•
=(cosθ+
)×
=1+
cosθ,
∵-1≤cosθ≤1,
∴
•
的取值范围是[1-
,1+
]
故答案为:[1-
,1+
]
∵|MN|=
| 2 |
∴M(-
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
设Q(cosθ,sinθ)
则
| MQ |
| ||
| 2 |
| ||
| 2 |
| MN |
| 2 |
∴
| MQ |
| MN |
| ||
| 2 |
| 2 |
| 2 |
∵-1≤cosθ≤1,
∴
| MQ |
| MN |
| 2 |
| 2 |
故答案为:[1-
| 2 |
| 2 |
点评:本题主要考查了向量的数量积的运算,关键是建立合适的平面直角坐标系,属于中档题.

练习册系列答案
相关题目

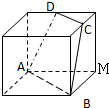 如图,正方体的棱长为1,C、D分别是两条棱的中点,A、B、M是顶点,那么点M到截面ABCD的距离是
如图,正方体的棱长为1,C、D分别是两条棱的中点,A、B、M是顶点,那么点M到截面ABCD的距离是 如图,设椭圆C:
如图,设椭圆C: