题目内容
在平面直角坐标系xOy中,椭圆C:
+
=1(a>b>0)的离心率为
,直线y=x被椭圆C截得的线段长为
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过原点的直线与椭圆C交于A,B两点(A,B不是椭圆C的顶点).点D在椭圆C上,且AD⊥AB,直线BD与x轴、y轴分别交于M,N两点.
(i)设直线BD,AM的斜率分别为k1,k2,证明存在常数λ使得k1=λk2,并求出λ的值;
(ii)求△OMN面积的最大值.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
4
| ||
| 5 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)过原点的直线与椭圆C交于A,B两点(A,B不是椭圆C的顶点).点D在椭圆C上,且AD⊥AB,直线BD与x轴、y轴分别交于M,N两点.
(i)设直线BD,AM的斜率分别为k1,k2,证明存在常数λ使得k1=λk2,并求出λ的值;
(ii)求△OMN面积的最大值.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程,圆锥曲线中的最值与范围问题
分析:(Ⅰ)由椭圆离心率得到a,b的关系,化简椭圆方程,和直线方程联立后求出交点的横坐标,把弦长用交点横坐标表示,则a的值可求,进一步得到b的值,则椭圆方程可求;
(Ⅱ)(i)设出A,D的坐标分别为(x1,y1)(x1y1≠0),(x2,y2),用A的坐标表示B的坐标,把AB和AD的斜率都用A的坐标表示,写出直线AD的方程,和椭圆方程联立后利用根与系数关系得到AD横纵坐标的和,求出AD中点坐标,则BD斜率可求,再写出BD所在直线方程,取y=0得到M点坐标,由两点求斜率得到AM的斜率,由两直线斜率的关系得到λ的值;
(ii)由BD方程求出N点坐标,结合(i)中求得的M的坐标得到△OMN的面积,然后结合椭圆方程利用基本不等式求最值.
(Ⅱ)(i)设出A,D的坐标分别为(x1,y1)(x1y1≠0),(x2,y2),用A的坐标表示B的坐标,把AB和AD的斜率都用A的坐标表示,写出直线AD的方程,和椭圆方程联立后利用根与系数关系得到AD横纵坐标的和,求出AD中点坐标,则BD斜率可求,再写出BD所在直线方程,取y=0得到M点坐标,由两点求斜率得到AM的斜率,由两直线斜率的关系得到λ的值;
(ii)由BD方程求出N点坐标,结合(i)中求得的M的坐标得到△OMN的面积,然后结合椭圆方程利用基本不等式求最值.
解答:
解:(Ⅰ)由题意知,
=
=
,则a2=4b2.
∴椭圆C的方程可化为x2+4y2=a2.
将y=x代入可得x=±
,
因此
×
=
,解得a=2.
则b=1.
∴椭圆C的方程为
+y2=1;
(Ⅱ)(i)设A(x1,y1)(x1y1≠0),D(x2,y2),
则B(-x1,-y1).
∵直线AB的斜率kAB=
,
又AB⊥AD,
∴直线AD的斜率kAD=-
.
设AD方程为y=kx+m,
由题意知k≠0,m≠0.
联立
,得(1+4k2)x2+8kmx+4m2-4=0.
∴x1+x2=-
.
因此y1+y2=k(x1+x2)+2m=
.
由题意可得k1=
=-
=
.
∴直线BD的方程为y+y1=
(x+x1).
令y=0,得x=3x1,即M(3x1,0).
可得k2=-
.
∴k1=-
k2,即λ=-
.
因此存在常数λ=-
使得结论成立.
(ii)直线BD方程为y+y1=
(x+x1),
令x=0,得y=-
y1,即N(0,-
y1).
由(i)知M(3x1,0),
可得△OMN的面积为S=
×3×|x1|×
|y1|=
|
||y1|≤
(
+y12)=
.
当且仅当
=|y1|=
时等号成立.
∴△OMN面积的最大值为
.
| c |
| a |
| ||
| a |
| ||
| 2 |
∴椭圆C的方程可化为x2+4y2=a2.
将y=x代入可得x=±
| ||
| 5 |
因此
| 2 |
2
| ||
| 5 |
4
| ||
| 5 |
则b=1.
∴椭圆C的方程为
| x2 |
| 4 |
(Ⅱ)(i)设A(x1,y1)(x1y1≠0),D(x2,y2),
则B(-x1,-y1).
∵直线AB的斜率kAB=
| y1 |
| x1 |
又AB⊥AD,
∴直线AD的斜率kAD=-
| x1 |
| y1 |
设AD方程为y=kx+m,
由题意知k≠0,m≠0.
联立
|
∴x1+x2=-
| 8mk |
| 1+4k2 |
因此y1+y2=k(x1+x2)+2m=
| 2m |
| 1+4k2 |
由题意可得k1=
| y1+y2 |
| x1+x2 |
| 1 |
| 4k |
| y1 |
| 4x1 |
∴直线BD的方程为y+y1=
| y1 |
| 4x1 |
令y=0,得x=3x1,即M(3x1,0).
可得k2=-
| y1 |
| 2x1 |
∴k1=-
| 1 |
| 2 |
| 1 |
| 2 |
因此存在常数λ=-
| 1 |
| 2 |
(ii)直线BD方程为y+y1=
| y1 |
| 4x1 |
令x=0,得y=-
| 3 |
| 4 |
| 3 |
| 4 |
由(i)知M(3x1,0),
可得△OMN的面积为S=
| 1 |
| 2 |
| 3 |
| 4 |
| 9 |
| 4 |
| x1 |
| 2 |
| 9 |
| 8 |
| x12 |
| 4 |
| 9 |
| 8 |
当且仅当
| |x1| |
| 2 |
| ||
| 2 |
∴△OMN面积的最大值为
| 9 |
| 8 |
点评:本题考查椭圆方程的求法,主要考查了直线与椭圆的位置关系的应用,直线与曲线联立,根据方程的根与系数的关系解题,是处理这类问题的最为常用的方法,但圆锥曲线的特点是计算量比较大,要求考试具备较强的运算推理的能力,是压轴题.

练习册系列答案
相关题目
若定义在R上的偶函数f(x)满足f(x+2)=f(x),且当x∈[0,1]时,f(x)=x,则方程f(x)=log3|x|的解个数是( )
| A、9个 | B、2个 |
| C、4 个 | D、6个 |
设U=R,P={x|x<1},Q={x|x2≥4},则P∩∁UQ=( )
| A、{x|-1<x<2} |
| B、{x|-2<x<1} |
| C、{x|1<x<2} |
| D、{x|-2<x<2} |
 如图,已知二面角α-MN-β的大小为60°,菱形ABCD在面β内,A、B两点在棱MN上,∠BAD=60°,E是AB的中点,DO⊥面α,垂足为O.
如图,已知二面角α-MN-β的大小为60°,菱形ABCD在面β内,A、B两点在棱MN上,∠BAD=60°,E是AB的中点,DO⊥面α,垂足为O.
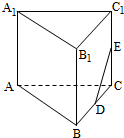 在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形
在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形