题目内容
一盒中装有9张各写有一个数字的卡片,其中4张卡片上的数字是1,3张卡片上的数字是2,2张卡片上的数字是3,从盒中任取3张卡片.
(Ⅰ)求所取3张卡片上的数字完全相同的概率;
(Ⅱ)X表示所取3张卡片上的数字的中位数,求X的分布列与数学期望.(注:若三个数字a,b,c满足a≤b≤c,则称b为这三个数的中位数.)
(Ⅰ)求所取3张卡片上的数字完全相同的概率;
(Ⅱ)X表示所取3张卡片上的数字的中位数,求X的分布列与数学期望.(注:若三个数字a,b,c满足a≤b≤c,则称b为这三个数的中位数.)
考点:离散型随机变量的期望与方差,古典概型及其概率计算公式
专题:常规题型
分析:第一问是古典概型的问题,要先出基本事件的总数和所研究的事件包含的基本事件个数,然后代入古典概型概率计算公式即可,相对简单些;
第二问应先根据题意求出随机变量X的所有可能取值,此处应注意所取三张卡片可能来自于相同数字(如1或2)或不同数字(1和2、1和3、2和3三类)的卡片,因此应按卡片上的数字相同与否进行分类分析,然后计算出每个随机变量所对应事件的概率,最后将分布列以表格形式呈现.
第二问应先根据题意求出随机变量X的所有可能取值,此处应注意所取三张卡片可能来自于相同数字(如1或2)或不同数字(1和2、1和3、2和3三类)的卡片,因此应按卡片上的数字相同与否进行分类分析,然后计算出每个随机变量所对应事件的概率,最后将分布列以表格形式呈现.
解答:
解:(Ⅰ)由古典概型的概率计算公式得所求概率为
P=
=
,
(Ⅱ)由题意知X的所有可能取值为1,2,3,且
P(X=1)=
=
,
P(X=2)=
=
,
P(X=3)=
=
,
所以X的分布列为:
所以E(X)=1×
+2×
+3×
=
.
P=
| ||||
|
| 5 |
| 84 |
(Ⅱ)由题意知X的所有可能取值为1,2,3,且
P(X=1)=
| ||||||
|
| 17 |
| 42 |
P(X=2)=
| ||||||||||||
|
| 43 |
| 84 |
P(X=3)=
| ||||
|
| 1 |
| 12 |
所以X的分布列为:
| X | 1 | 2 | 3 | ||||||
| P |
|
|
|
| 17 |
| 42 |
| 43 |
| 84 |
| 1 |
| 12 |
| 47 |
| 28 |
点评:本题属于中档题,关键是要弄清涉及的基本事件以及所研究的事件是什么才能解答好第一问;第二问的只要是准确记住了中位数的概念,应该说完成此题基本没有问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知集合A={-1,0,1,2,3},B={x||x-1|<2},则A∩∁RB=( )
| A、{0,1,2} |
| B、{-1,3} |
| C、{1,2} |
| D、{-1,0,3} |
已知i是虚数单位,i2=-1,则复数
在复平面上对应点的坐标是( )
| 5i |
| 2-i |
| A、(-1,2) |
| B、(1,-2) |
| C、(1,2) |
| D、(-1,-2) |
 如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,AB⊥B1C.
如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,AB⊥B1C.
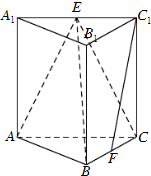 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.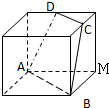 如图,正方体的棱长为1,C、D分别是两条棱的中点,A、B、M是顶点,那么点M到截面ABCD的距离是
如图,正方体的棱长为1,C、D分别是两条棱的中点,A、B、M是顶点,那么点M到截面ABCD的距离是