题目内容

证明：函数f（x）=
ex-e-x
2
为增函数．
考点：函数单调性的判断与证明
专题：函数的性质及应用
分析：利用指数函数的性质来进行证明，首先根据函数的性质ex在x∈R为单调递增函数，e-x在x∈R为单调递减函数，则：ex-e-x为单调递增函数，从而得到结论．
解答： 证明：函数f（x）=
ex-e-x
2
的定义域为：x∈R
根据函数的性质ex在x∈R为单调递增函数，e-x在x∈R为单调递减函数
则：ex-e-x为单调递增函数，
从而得到：f（x）=
ex-e-x
2
在在x∈R为单调递增函数
点评：本题考查的知识点：函数单调性的证明利用指数函数的性质来证明．
练习册系列答案
相关题目
曲线y=e2x-x在点（0，1）处的切线方程为（　　）
A、y=
1
2
x+1
B、y=1
C、y=2x-1
D、y=x+1
若函数f（x）=x+
1
x
，设集合A={x|2≤f（x）≤
5
2
}，U=R，则集合∁UA=
 
．
已知f（x）=lg（x2-2ax-a）在区间（-∞，-3）上是减函数，求实数a的取值范围．
已知函数f（x）=lnx-x-
a
x
，a∈R．
（1）若f（x）在[1，2]上单调递增，求a的取值范围；
（2）讨论f（x）的单调性．
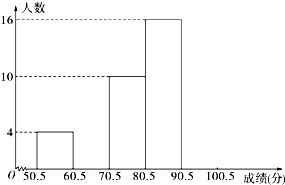为了让学生了解环保知识，增强环保意识，某中学举行了一次“环保知识竞赛”，共有900名学生参加了这次竞赛．为了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分均为整数，满分为100分）进行统计．请你根据尚未完成并有局部污损的频率分布表和频率分布直方图，解答下列问题：
分组频数频率
50.5～60.540.08
60.5～70.50.16
70.5～80.510
80.5～90.5160.32
90.5～100.5
合计50
（1）请填充频率分布表的空格，并补全频率分布直方图；
（2）若成绩在75.5～85.5分的学生为二等奖，请你估计获得二等奖的人数；
（3）用分层抽样的方法从80分以上（不包括80分）的学生中抽取了7人进行试卷分析，再从这7人中选取2人进行经验汇报，求选出的2人至少有1人在[90.5，100.5]的概率．
已知二次函数y=f（x），当x=2时函数取最小值-1，且f（1）+f（4）=3．
（1）求f（x）的解析式；
（2）若g（x）=f（x）-kx在区间[1，4]上不单调，求实数k的取值范围．
某校高三年级有男学生105人，女学生126人，教师42人，用分层抽样的方法从中抽取13人进行问卷调查，设其中某项问题的选择，分别为“同意”、“不同意”两种，且每人都做了一种选择，下面表格中提供了被调查人答卷情况的部分信息．
同意不同意合计
教师1  
女学生 4 
男学生 2 
（1）完成此统计表；
（2）估计高三年级学生“同意”的人数；
（3）从被调查的女学生中选取2人进行访谈，设“同意”的人数为ξ，求Eξ．
设函数f（x）=
x+1
x+a
在区间（3，+∞）上是减函数，则实数a的取值范围是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网