题目内容
已知圆C经过A(2,3),B(0,3)两点,且与直线x+y-5=0相切,
(1)求圆C的标准方程;
(2)在直线x+y+1=0上任取一点P,过P点作圆C的切线,切点为Q,当|PQ|最小时,求切线PQ的斜率.
(1)求圆C的标准方程;
(2)在直线x+y+1=0上任取一点P,过P点作圆C的切线,切点为Q,当|PQ|最小时,求切线PQ的斜率.
考点:直线和圆的方程的应用
专题:综合题,直线与圆
分析:(1)设圆心坐标为(1,b),半径为r,利用圆与直线x+y-5=0相切,建立方程,求出圆心与半径,即可求圆C的标准方程;
(2)当|PQ|最小时,CP垂直于直线x+y+1=0,故可得直线CP的方程,与直线x+y+1=0,联立,可得P的坐标,设出切线PQ的方程,利用圆心到直线的距离d=r,即可得出结论.
(2)当|PQ|最小时,CP垂直于直线x+y+1=0,故可得直线CP的方程,与直线x+y+1=0,联立,可得P的坐标,设出切线PQ的方程,利用圆心到直线的距离d=r,即可得出结论.
解答:
解:(1)设圆心坐标为(1,b),半径为r,则
∵圆与直线x+y-5=0相切,
∴
=
=r,
∴b=2,r=
,
∴圆C的标准方程为(x-1)2+(y-2)2=2;
(2)当|PQ|最小时,CP垂直于直线x+y+1=0,故可得直线CP的方程为y-2=x-1,即x-y+1=0,
与直线x+y+1=0,联立,可得P(-1,0),
设切线PQ的斜率为k,则切线PQ的方程为y=k(x+1),即kx-y-k=0,
∴圆心到直线的距离d=
=
,
∴k=±1.
∵圆与直线x+y-5=0相切,
∴
| |1+b-5| | ||
|
| 1+(b-3)2 |
∴b=2,r=
| 2 |
∴圆C的标准方程为(x-1)2+(y-2)2=2;
(2)当|PQ|最小时,CP垂直于直线x+y+1=0,故可得直线CP的方程为y-2=x-1,即x-y+1=0,
与直线x+y+1=0,联立,可得P(-1,0),
设切线PQ的斜率为k,则切线PQ的方程为y=k(x+1),即kx-y-k=0,
∴圆心到直线的距离d=
| |k-2-k| | ||
|
| 2 |
∴k=±1.
点评:本题考查圆的标准方程,考查直线与圆的位置关系,考查学生分析解决问题的能力,考查学生的计算能力,确定当|PQ|最小时,CP垂直于直线x+y+1=0是关键.

练习册系列答案
相关题目
 用5种不同颜色给图中A、B、C、D四个区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不同,则不同的涂色方法种数为( )
用5种不同颜色给图中A、B、C、D四个区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不同,则不同的涂色方法种数为( )| A、120 | B、160 |
| C、180 | D、240 |
圆柱的侧面展开图是一个边长为2和4的矩形,则圆柱的体积为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、8 |




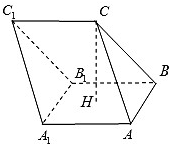 如图,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心,AA1=2,CH⊥平面AA1B1B,且CH=3.
如图,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心,AA1=2,CH⊥平面AA1B1B,且CH=3.