题目内容
若直线(a+2)x+(1-a)y=a2(a>0)与直线(a-1)x+(2a+3)y+2=0互相垂直,则a等于( )
| A、1 | B、-1 | C、±1 | D、-2 |
考点:直线的一般式方程与直线的垂直关系
专题:直线与圆
分析:分类讨论:两条直线的斜率存在与不存在两种情况,由于a>0,因此分a=1和a>0且a≠1讨论,再利用相互垂直的直线斜率之间的关系即可.
解答:
解:①当a=1时,利用直线的方程分别化为:3x=1,5y+2=0,此时两条直线相互垂直.
②∵a>0,当a≠1时,此两条直线的斜率分别为-
,-
.
∵两条直线相互垂直,
∴(-
)•(-
)=-1,化为a2=1,
∵a≠1,
解得a=-1.
综上可知:a=±1.
故选:C.
②∵a>0,当a≠1时,此两条直线的斜率分别为-
| a+2 |
| 1-a |
| a-1 |
| 2a+3 |
∵两条直线相互垂直,
∴(-
| a+2 |
| 1-a |
| a-1 |
| 2a+3 |
∵a≠1,
解得a=-1.
综上可知:a=±1.
故选:C.
点评:本题考查了相互垂直的直线斜率之间的关系、分类讨论思想方法,属于基础题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
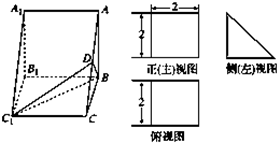 直三棱柱ABC-A1B1C1的直观图及三视图如图所示,D为AC的中点,则下列命题是假命题的是( )
直三棱柱ABC-A1B1C1的直观图及三视图如图所示,D为AC的中点,则下列命题是假命题的是( )| A、AB1∥平面BDC1 | ||
| B、A1C⊥平面BDC1 | ||
| C、直三棱柱的体积V=4 | ||
D、直三棱柱的外接球的表面积为4
|
设有一组圆Ck:(x-k+1)2+(y-3k)2=2k4(k∈N*).下列四个命题,正确的有几个( )
①存在一条定直线与所有的圆均相切;
②存在一条定直线与所有的圆均相交;
③存在一条定直线与所有的圆均不相交;
④所有的圆均不经过原点.
①存在一条定直线与所有的圆均相切;
②存在一条定直线与所有的圆均相交;
③存在一条定直线与所有的圆均不相交;
④所有的圆均不经过原点.
| A、1 | B、2 | C、3 | D、4 |
 用5种不同颜色给图中A、B、C、D四个区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不同,则不同的涂色方法种数为( )
用5种不同颜色给图中A、B、C、D四个区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不同,则不同的涂色方法种数为( )| A、120 | B、160 |
| C、180 | D、240 |
 座落于我市红梅公园边的天宁宝塔堪称中华之最,也堪称佛塔世界之最.如图,已知天宁宝塔AB高度为150米,某大楼CD高度为90米,从大楼CD顶部C看天宁宝塔AB的张角∠ACB=45°,求天宁宝塔AB与大楼CD底部之间的距离BD.
座落于我市红梅公园边的天宁宝塔堪称中华之最,也堪称佛塔世界之最.如图,已知天宁宝塔AB高度为150米,某大楼CD高度为90米,从大楼CD顶部C看天宁宝塔AB的张角∠ACB=45°,求天宁宝塔AB与大楼CD底部之间的距离BD.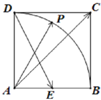 如图所示,在正方形ABCD中,E为AB的中点,P是以A为圆心,AB为半径的圆弧BD上的任意一点,设∠PAB=θ,向量
如图所示,在正方形ABCD中,E为AB的中点,P是以A为圆心,AB为半径的圆弧BD上的任意一点,设∠PAB=θ,向量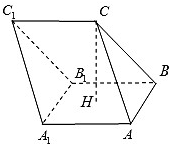 如图,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心,AA1=2,CH⊥平面AA1B1B,且CH=3.
如图,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心,AA1=2,CH⊥平面AA1B1B,且CH=3.