题目内容
直线与双曲线x2-4y2=4交于A、B两点,若线段AB的中点坐标为(8,1),则直线的方程为 .
考点:直线与圆锥曲线的关系,直线的一般式方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:设出A,B的坐标,代入双曲线方程,两式相减,根据中点的坐标可知x1+x2和y1+y2的值,进而求得直线AB的斜率,根据点斜式求得直线的方程.
解答:
解:设A(x1,y1),B(x2,y2),则x1+x2=16,y1+y2=2,
∵x12-4y12=4,x22-4y22=4,
∴16(x1-x2)-8(y1-y2)=0,
∴kAB=
=2,
∴直线的方程为y-1=2(x-8),即2x-y-15=0.
故答案为:2x-y-15=0.
∵x12-4y12=4,x22-4y22=4,
∴16(x1-x2)-8(y1-y2)=0,
∴kAB=
| y1-y2 |
| x1-x2 |
∴直线的方程为y-1=2(x-8),即2x-y-15=0.
故答案为:2x-y-15=0.
点评:涉及弦长的中点问题,常用“点差法”设而不求,将弦所在直线的斜率、弦的中点坐标联系起来,相互转化.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
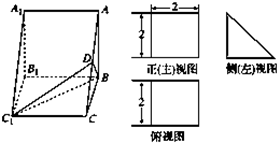 直三棱柱ABC-A1B1C1的直观图及三视图如图所示,D为AC的中点,则下列命题是假命题的是( )
直三棱柱ABC-A1B1C1的直观图及三视图如图所示,D为AC的中点,则下列命题是假命题的是( )| A、AB1∥平面BDC1 | ||
| B、A1C⊥平面BDC1 | ||
| C、直三棱柱的体积V=4 | ||
D、直三棱柱的外接球的表面积为4
|
圆柱的侧面展开图是一个边长为2和4的矩形,则圆柱的体积为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、8 |