题目内容
已知A(1,0,0),B(0,1,1),C(1,1,0),D(1,2,0),E(0,0,1),则直线DE与平面ABC的位置关系是 .
考点:空间中直线与平面之间的位置关系,共线向量与共面向量
专题:空间位置关系与距离
分析:求出向量
,
,
,如果满足共面向量定理,即可判断直线与平面的位置关系.
| AB |
| AC |
| DE |
解答:
解:A(1,0,0),B(0,1,1),C(1,1,0),D(1,2,0),E(0,0,1),
∴向量
=(-1,1,1),
=(0,1,0),
=(-1.-2,1),显然
=
-3
,∴向量
,
,
,共面.
=
,∴A、C、D共线,
可得A、B、C、D、E在一个平面内.
∴直线DE在平面ABC内.
故答案为:直线DE在平面ABC内.
∴向量
| AB |
| AC |
| DE |
| DE |
| AB |
| AC |
| AB |
| AC |
| DE |
| AC |
| CD |
可得A、B、C、D、E在一个平面内.
∴直线DE在平面ABC内.
故答案为:直线DE在平面ABC内.
点评:本题考查直线与平面的位置关系,共面向量定理的应用,注意直线与平面平行与直线在平面内的区别.

练习册系列答案
相关题目
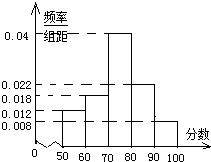 某次素质测试,随机抽取了部分学生的成绩,得到如图所示的频率分布直方图.
某次素质测试,随机抽取了部分学生的成绩,得到如图所示的频率分布直方图.