题目内容
在区间[0,9]上随机取一实数x,则该实数x满足不等式1≤|x|≤2的概率为 .
考点:几何概型
专题:计算题,概率与统计
分析:解不等式1≤|x|≤2,可得-2≤x≤-1或1≤x≤2,以长度为测度,即可求在区间[0,9]上随机取一实数x,该实数x满足不等式1≤|x|≤2的概率.
解答:
解:本题属于几何概型
解不等式1≤|x|≤2,可得-2≤x≤-1或1≤x≤2,又在区间[0,9]上,∴1≤x≤2
∴在区间[0,9]上随机取一实数x,该实数x满足不等式1≤丨x丨≤2的概率为
.
故答案为:
.
解不等式1≤|x|≤2,可得-2≤x≤-1或1≤x≤2,又在区间[0,9]上,∴1≤x≤2
∴在区间[0,9]上随机取一实数x,该实数x满足不等式1≤丨x丨≤2的概率为
| 1 |
| 9 |
故答案为:
| 1 |
| 9 |
点评:本题考查几何概型,解题的关键是解不等式,确定其测度.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
已知函数f(x)=x3+ax+1是R上的单调递增函数,则a的取值范围是( )
| A、a≥0 | B、a≥-1 |
| C、a<0 | D、a<-1 |
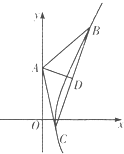 如图,B,C两点在双曲线x2-
如图,B,C两点在双曲线x2-