题目内容
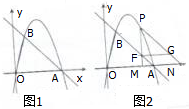 如图1,在平面直角坐标系中,点O为坐标原点,直线y=-x+4与x轴交与点A,过点A的抛物线y=ax2+bx与直线y=-x+4交与另一点B,B的横坐标为1.
如图1,在平面直角坐标系中,点O为坐标原点,直线y=-x+4与x轴交与点A,过点A的抛物线y=ax2+bx与直线y=-x+4交与另一点B,B的横坐标为1.(1)点C为抛物线的顶点,点D为直线AB上一点,点E为该抛物线上一点,且D、E两点的纵坐标都为1,求△CDE面积.
(2)如图2,P为直线AB上方的抛物线上一点(点P不与点A、B重合),PM⊥x轴于点M,交线段AB于点F,PN∥AB,交x轴于点N,过点F作FG∥x轴,交PN于点G,设点M的坐标为(m,0),FG的长度为d,求d与m之间的函数关系式及FG长度的最大值,且求出此时P点坐标.
考点:直线与圆锥曲线的综合问题
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:(1)令y=0,可得A(4,0),令x=1,可得B(1,3),再代入抛物线方程,得到方程组,解出a,b,即可得到抛物线方程,进而得到C,D,E的坐标,再由面积公式,即可得到△CDE面积;
(2)由M的坐标,即可得到P,F的坐标,再由PN∥AB,得到直线PN的方程,即可得到G的坐标,即可得到距离d,再由m∈(1,4),求出最大值,以及点P的坐标.
(2)由M的坐标,即可得到P,F的坐标,再由PN∥AB,得到直线PN的方程,即可得到G的坐标,即可得到距离d,再由m∈(1,4),求出最大值,以及点P的坐标.
解答:
解:(1)由于直线y=-x+4与x轴交于点A,则A(4,0).
由于过点A的抛物线y=ax2+bx与直线y=-x+4交于另一点B,B的横坐标为1,
则B(1,3).
由
,解得
,
则有抛物线y=-x2+4x,
即有顶点C(2,4),D(3,1),E(2±
,1)
则S△DEC=
×3×|2±
-3|=
(
±1);
(2)由于M的坐标为(m,0),
则P(m,4m-m2),F(m,4-m),
由于PN∥AB,
则直线PN:y-4m+m2=-(x-m),即y=-x+5m-m2,
当y=4-m时,x=6m-m2-4,
即有G的坐标为(6m-m2-4,4-m),
则d=|6m-m2-4-m|=|-m2+5m-4|,
由于m∈(1,4),
则-m2+5m-4>0
则有,d=-m2+5m-4.
当m=
时,dmax=-
+
-4=
,
把m=
代入得P点坐标(
,
).
由于过点A的抛物线y=ax2+bx与直线y=-x+4交于另一点B,B的横坐标为1,
则B(1,3).
由
|
|
则有抛物线y=-x2+4x,
即有顶点C(2,4),D(3,1),E(2±
| 3 |
则S△DEC=
| 1 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
(2)由于M的坐标为(m,0),
则P(m,4m-m2),F(m,4-m),
由于PN∥AB,
则直线PN:y-4m+m2=-(x-m),即y=-x+5m-m2,
当y=4-m时,x=6m-m2-4,
即有G的坐标为(6m-m2-4,4-m),
则d=|6m-m2-4-m|=|-m2+5m-4|,
由于m∈(1,4),
则-m2+5m-4>0
则有,d=-m2+5m-4.
当m=
| 5 |
| 2 |
| 25 |
| 4 |
| 25 |
| 2 |
| 9 |
| 4 |
把m=
| 5 |
| 2 |
| 5 |
| 2 |
| 15 |
| 4 |
点评:本题考查抛物线的方程和运用,考查直线方程及运用,考查运算能力,属于中档题.

练习册系列答案
相关题目
已知集合M中含有3个元素:0,x2,-x,则x满足的条件是( )
| A、x≠0 |
| B、x≠-1 |
| C、x≠0且x≠-1 |
| D、x≠0且x≠1 |
已知四面体P-ABC中,PA=4,AC=2
,PB=PC=2
,PA⊥平面PBC,则四面体P-ABC的内切球半径与外接球半径的比( )
| 7 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设全集为R,集合A={x|x2-9<0},B={x|-1<x≤5},则A∩B=( )
| A、(3,5] |
| B、(-1,3) |
| C、(-3,-1) |
| D、(-3,5] |