题目内容
已知不等式x2-4x+3＜0的解集是A．
（1）设函数f（x）=log2（a-x）（a∈R）的定义域为集合B，若A⊆B，求a的取值范围；
（2）设不等式ax2-2x-2a＞0（a∈R且a≠0）的解集为C，若A∩C≠∅，求a的取值范围．
（1）设函数f（x）=log2（a-x）（a∈R）的定义域为集合B，若A⊆B，求a的取值范围；
（2）设不等式ax2-2x-2a＞0（a∈R且a≠0）的解集为C，若A∩C≠∅，求a的取值范围．
考点：二次函数的性质
专题：函数的性质及应用
分析：（1）解不等式x2-4x+3＜0可得A由题意可得B=（-∞，a）由A⊆B 结合数轴可求a的取值范围；
（2）（法一）设g（x）=ax2-2x-2a，由A∩C≠φ可知1，3∈C，则①a＞0时，g（3）＞0；②a＜0时，g（1）＞0可求a的范围，
（法二）由f（x）为二次函数，可得a≠0，令f（x）=0，解得其两根为x1=
-
＜0，x2=
+
＞0，
①当a＞0时，A={x|x＜x1或x＞x2}，又A∩C≠∅，则满足：x2＜3，②当a＜0时，A={x|x1＜x＜x2}，满足x2＞1，从而可求a的范围．
（2）（法一）设g（x）=ax2-2x-2a，由A∩C≠φ可知1，3∈C，则①a＞0时，g（3）＞0；②a＜0时，g（1）＞0可求a的范围，
（法二）由f（x）为二次函数，可得a≠0，令f（x）=0，解得其两根为x1=
| 1 |
| a |
2+
|
| 1 |
| a |
2+
|
①当a＞0时，A={x|x＜x1或x＞x2}，又A∩C≠∅，则满足：x2＜3，②当a＜0时，A={x|x1＜x＜x2}，满足x2＞1，从而可求a的范围．
解答：
解：解不等式x2-4x+3＜0得：A={x|1＜x＜3}，
（1）由a-x＞0，解得：x＜a，∴B={x|x＜a}，
若A⊆B，则a≥3，
∴a的范围是：{a|a≥3}．
（2）设g（x）=ax2-2x-2a1
①a＞0时，g（3）＞0⇒a＞
；
②a＜0时，g（1）＞0⇒a＜-2
则a的取值范围是（-∞，-2）∪（
，+∞）．
另解：∵f（x）为二次函数，∴a≠0，令f（x）=0，解得其两根为x1=
-
＜0，x2=
+
＞0
①当a＞0时，A={x|x＜x1或x＞x2}，又知集合B={x|1＜x＜3}，A∩C≠∅，则满足：x2＜3，即
+
＜3，
∴a＞
；
②当a＜0时，A={x|x1＜x＜x2}，A∩C≠∅其满足x2＞1，即
+
＞1，解得a＜-2．
综上所述，使A∩C≠∅成立的a的取值范围是（-∞，-2）∪（
，+∞）．
（1）由a-x＞0，解得：x＜a，∴B={x|x＜a}，
若A⊆B，则a≥3，
∴a的范围是：{a|a≥3}．
（2）设g（x）=ax2-2x-2a1
①a＞0时，g（3）＞0⇒a＞
| 6 |
| 7 |
②a＜0时，g（1）＞0⇒a＜-2
则a的取值范围是（-∞，-2）∪（
| 6 |
| 7 |
另解：∵f（x）为二次函数，∴a≠0，令f（x）=0，解得其两根为x1=
| 1 |
| a |
2+
|
| 1 |
| a |
2+
|
①当a＞0时，A={x|x＜x1或x＞x2}，又知集合B={x|1＜x＜3}，A∩C≠∅，则满足：x2＜3，即
| 1 |
| a |
2+
|
∴a＞
| 6 |
| 7 |
②当a＜0时，A={x|x1＜x＜x2}，A∩C≠∅其满足x2＞1，即
| 1 |
| a |
2+
|
综上所述，使A∩C≠∅成立的a的取值范围是（-∞，-2）∪（
| 6 |
| 7 |
点评：本题目主要考查了二次不等式的解法，对数函数的定义域的求解及二次函数与二次不等式、二次方程之间的相互转化，结合之间的包含关系的应用．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
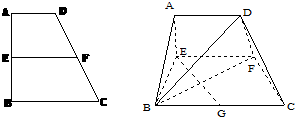已知梯形ABCD中，AD∥BC，∠ABC=∠BAD=
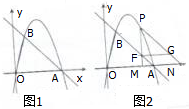如图1，在平面直角坐标系中，点O为坐标原点，直线y=-x+4与x轴交与点A，过点A的抛物线y=ax2+bx与直线y=-x+4交与另一点B，B的横坐标为1．