题目内容
已知数列{an}的前n项和为Sn,且Sn满足Sn=2an-2.
(1)求{an}的通项;
(2)若{bn}满足b1=1,
-
=1,求数列{an
}的前n项和.
(1)求{an}的通项;
(2)若{bn}满足b1=1,
| bn+1 |
| n+1 |
| bn |
| n |
| bn |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)根据Sn=2an-2,n∈N*得到当n≥2时,Sn-1=2an-1-2,两式相减得an=2an-1,求出首项,再求出等差数列{an}的通项公式;
(2)利用题意和等比数列的定义,求出数列{bn}的通项公式,再求出an
,利用错位相减法能求出数列{an
}的前n项和.
(2)利用题意和等比数列的定义,求出数列{bn}的通项公式,再求出an
| bn |
| bn |
解答:
解:(1)由题意得,Sn=2an-2,
则当n≥2时,Sn-1=2an-1-2,
两式相减得an=Sn-Sn-1=2an-2an-1,即an=2an-1,
令n=1得,a1=2a1-2,解得a1=2,
因此{an}是首项为2,公比为2的等比数列,
所以an=2×2n-1=2n;
(2)因为
-
=1,b1=1,
所以数列{
}是首项为1,公差为1的等差数列,
则
=1+(n-1)×1=n,即bn=n2,
所以an
=2n•
=n•2n,
设数列{an
}的前n项和为Tn,
则Tn=1×2+2×22+3×23+…+n×2n ①,
2Tn=1×22+2×23+3×24+…+n×2n+1 ②,
①-②得,-Tn=2+22+23+24+…+2n-n×2n+1
=
-n×2n+1=(-n+1)•2n+1-2
所以Tn=(n-1)•2n+1+2,
故数列{an
}的前n项和是(n-1)•2n+1+2.
则当n≥2时,Sn-1=2an-1-2,
两式相减得an=Sn-Sn-1=2an-2an-1,即an=2an-1,
令n=1得,a1=2a1-2,解得a1=2,
因此{an}是首项为2,公比为2的等比数列,
所以an=2×2n-1=2n;
(2)因为
| bn+1 |
| n+1 |
| bn |
| n |
所以数列{
| bn |
| n |
则
| bn |
| n |
所以an
| bn |
| n2 |
设数列{an
| bn |
则Tn=1×2+2×22+3×23+…+n×2n ①,
2Tn=1×22+2×23+3×24+…+n×2n+1 ②,
①-②得,-Tn=2+22+23+24+…+2n-n×2n+1
=
| 2(1-2n) |
| 1-2 |
所以Tn=(n-1)•2n+1+2,
故数列{an
| bn |
点评:本题考查数列的Sn与an的关系式的应用,等差、等比数列的定义、通项公式,以及数列的前n项和的求法:错位相减法的合理运用.

练习册系列答案
相关题目
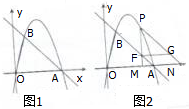 如图1,在平面直角坐标系中,点O为坐标原点,直线y=-x+4与x轴交与点A,过点A的抛物线y=ax2+bx与直线y=-x+4交与另一点B,B的横坐标为1.
如图1,在平面直角坐标系中,点O为坐标原点,直线y=-x+4与x轴交与点A,过点A的抛物线y=ax2+bx与直线y=-x+4交与另一点B,B的横坐标为1.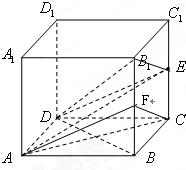 正方体ABCD-A1B1C1D1,AA1=2,E,F分别为棱CC1,BB1的中点.
正方体ABCD-A1B1C1D1,AA1=2,E,F分别为棱CC1,BB1的中点.