题目内容
设函数f(x)=x3+
x2+cx,(b,c∈R)
(1)b=2,c=-1,求y=|f(x)|的单调增区间;
(2)b=6,g(x)=|f(x)|,若g(x)≤kx对一切x∈[0,2]恒成立,求k的最小值h(c)的表达式.
| b |
| 2 |
(1)b=2,c=-1,求y=|f(x)|的单调增区间;
(2)b=6,g(x)=|f(x)|,若g(x)≤kx对一切x∈[0,2]恒成立,求k的最小值h(c)的表达式.
考点:利用导数研究函数的单调性
专题:计算题,选作题,导数的综合应用
分析:(1)由题意,f(x)=x3+x2-x=x(x-
)(x-
),从而写出y=|f(x)|的表达式,对函数f(x)求导并由导数说明函数f(x)的单调性,进而有函数图象的变换写出函数的单调增区间;
(2)由题意,f(x)=x3+3x2+cx,若x=0,则对任意k,都有g(0)=0≤k•0成立;若x≠0,则即x∈(0,2]时,通过独立参数法化g(x)≤kx为k≥|x2+3x+c|,令m(x)=x2-3x+c,从而求|x2+3x+c|在[0,2]上的最大值,则将g(x)≤kx对一切x∈[0,2]恒成立化为k≥,|x2+3x+c|max,从而求出k的取值范围,再求k的最小值h(c)的表达式.
-1-
| ||
| 2 |
-1+
| ||
| 2 |
(2)由题意,f(x)=x3+3x2+cx,若x=0,则对任意k,都有g(0)=0≤k•0成立;若x≠0,则即x∈(0,2]时,通过独立参数法化g(x)≤kx为k≥|x2+3x+c|,令m(x)=x2-3x+c,从而求|x2+3x+c|在[0,2]上的最大值,则将g(x)≤kx对一切x∈[0,2]恒成立化为k≥,|x2+3x+c|max,从而求出k的取值范围,再求k的最小值h(c)的表达式.
解答:
解:(1)由题意,f(x)=x3+x2-x=x(x-
)(x-
),
则y=|f(x)|=
,
又∵f′(x)=3x2+2x-1=(3x-1)(x+1),
∴f(x)=x3-x2-x在(-∞,-1)上是增函数,在(-1,
)上是减函数,在(
,+∞)上是增函数,
∴y=|f(x)|的单调增区间有:(
,-1),(0,
),(
,+∞);
(2)由题意,f(x)=x3+3x2+cx,
若x=0,则对任意k,都有g(0)=0≤k•0成立;
若x≠0,则即x∈(0,2]时,
g(x)≤kx可化为k≥|x2+3x+c|,
令m(x)=x2+3x+c=(x+
)2-
+c,
∴m(x)=(x+
)2-
+c在[0,2]上的最小值为
m(0)=c,最大值为m(2)=7+c,
则当|c|>|7+c|,即c<-3.5时,|x2+3x+c|max=|c|=-c,
当|c|≤|7+c|,即c≥-3.5时,|x2-3x+c|max=|7+c|=7+c,
则k≥|x2+3x+c|,对一切x∈(0,2]恒成立可化为,
当c>-3.5时,k≥-c;当c≤-3.5时,k≥7+c;
则k的最小值h(c)=
.
-1-
| ||
| 2 |
-1+
| ||
| 2 |
则y=|f(x)|=
|
又∵f′(x)=3x2+2x-1=(3x-1)(x+1),
∴f(x)=x3-x2-x在(-∞,-1)上是增函数,在(-1,
| 1 |
| 3 |
| 1 |
| 3 |
∴y=|f(x)|的单调增区间有:(
-1-
| ||
| 2 |
| 1 |
| 3 |
-1+
| ||
| 2 |
(2)由题意,f(x)=x3+3x2+cx,
若x=0,则对任意k,都有g(0)=0≤k•0成立;
若x≠0,则即x∈(0,2]时,
g(x)≤kx可化为k≥|x2+3x+c|,
令m(x)=x2+3x+c=(x+
| 3 |
| 2 |
| 9 |
| 4 |
∴m(x)=(x+
| 3 |
| 2 |
| 9 |
| 4 |
m(0)=c,最大值为m(2)=7+c,
则当|c|>|7+c|,即c<-3.5时,|x2+3x+c|max=|c|=-c,
当|c|≤|7+c|,即c≥-3.5时,|x2-3x+c|max=|7+c|=7+c,
则k≥|x2+3x+c|,对一切x∈(0,2]恒成立可化为,
当c>-3.5时,k≥-c;当c≤-3.5时,k≥7+c;
则k的最小值h(c)=
|
点评:本题考查导数的综合应用,同时考查了函数图象的变换应用及恒成立问题的处理方法,化简与思路都比较难,属于难题.

练习册系列答案
相关题目
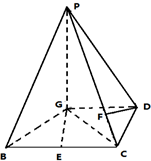 已知四棱锥P-GBCD中(如图),PG⊥平面GBCD,GD∥BC,GD=
已知四棱锥P-GBCD中(如图),PG⊥平面GBCD,GD∥BC,GD=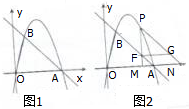 如图1,在平面直角坐标系中,点O为坐标原点,直线y=-x+4与x轴交与点A,过点A的抛物线y=ax2+bx与直线y=-x+4交与另一点B,B的横坐标为1.
如图1,在平面直角坐标系中,点O为坐标原点,直线y=-x+4与x轴交与点A,过点A的抛物线y=ax2+bx与直线y=-x+4交与另一点B,B的横坐标为1.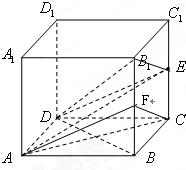 正方体ABCD-A1B1C1D1,AA1=2,E,F分别为棱CC1,BB1的中点.
正方体ABCD-A1B1C1D1,AA1=2,E,F分别为棱CC1,BB1的中点.