题目内容
已知向量
=（x，2），
=（-3，-5），
与
的夹角为钝角，则x的取值范围为 ．
| a |
| b |
| a |
| b |
考点：数量积表示两个向量的夹角
专题：平面向量及应用
分析：由题意可得
•
＜0，且
与
不共线，可得
，由此求得x的范围．
| a |
| b |
| a |
| b |
|
解答：
解：∵向量
=（x，2），
=（-3，-5），
与
的夹角为钝角，∴
•
＜0，且
与
不共线，
所以有
，解之x∈（-
，-
）∪（
，+∞），
故答案为：（-
，-
）∪（
，+∞）．
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
所以有
|
| 10 |
| 3 |
| 6 |
| 5 |
| 6 |
| 5 |
故答案为：（-
| 10 |
| 3 |
| 6 |
| 5 |
| 6 |
| 5 |
点评：本题主要考查用两个向量的数量积表示两个向量的夹角，两个向量共线的性质，两个向量坐标形式的运算，属于基础题．
练习册系列答案
愉快的寒假南京出版社系列答案
相关题目
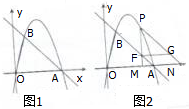如图1，在平面直角坐标系中，点O为坐标原点，直线y=-x+4与x轴交与点A，过点A的抛物线y=ax2+bx与直线y=-x+4交与另一点B，B的横坐标为1．
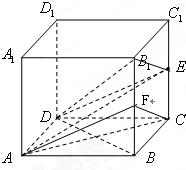正方体ABCD-A1B1C1D1，AA1=2，E，F分别为棱CC1，BB1的中点．椭圆2x2+3y2=6的焦距是（ ）
| A、2 | ||||
B、2（
| ||||
C、2
| ||||
D、2（
|