题目内容

已知函数f（x）=loga（x+
x2+1
），若f（-2）=3，则f（2）=
 
．
考点：函数奇偶性的性质,函数的值
专题：函数的性质及应用
分析：直接利用函数的奇偶性的性质，化简求值即可．
解答： 解：函数f（x）=loga（x+
x2+1
），f（-x）=loga（-x+
x2+1
）=-loga（x+
x2+1
）=-f（x），
所以函数f（x）是奇函数，
f（-2）=3，
∴f（2）=-f（-2）=-3．
故答案为：-3．
点评：本题考查函数的奇偶性的应用，函数值的求法，考查计算能力．
练习册系列答案
相关题目
已知函数f（x）=ax2-ax+3x+1在（0，1）内存在一个零点，则实数a的取值范围是
 
．
平面内动点P（x，y）与两定点A（-2，0），B（2，0）连级的斜率之积等于-
1
3
，若点P的轨迹为曲线E，过点（-1，0）作斜率不为零的直线BC交曲线E于点B、C．
（Ⅰ）求曲线E的方程；
（Ⅱ）求证：AB⊥AC；
（Ⅲ）求△ABC面积的最大值．
某次国际象棋比赛规定，胜一局得3分，平一局得1分，负一局得0分，某参赛队员比赛一局胜的概率为a，平局的概率为b，负的概率为c（a、b、c∈[0，1）），已知他比赛一局得分的数学期望为1，则ab的最大值为（　　）
A、
1
3
B、
1
2
C、
1
12
D、
1
6
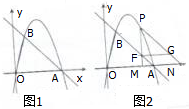如图1，在平面直角坐标系中，点O为坐标原点，直线y=-x+4与x轴交与点A，过点A的抛物线y=ax2+bx与直线y=-x+4交与另一点B，B的横坐标为1．
（1）点C为抛物线的顶点，点D为直线AB上一点，点E为该抛物线上一点，且D、E两点的纵坐标都为1，求△CDE面积．
（2）如图2，P为直线AB上方的抛物线上一点（点P不与点A、B重合），PM⊥x轴于点M，交线段AB于点F，PN∥AB，交x轴于点N，过点F作FG∥x轴，交PN于点G，设点M的坐标为（m，0），FG的长度为d，求d与m之间的函数关系式及FG长度的最大值，且求出此时P点坐标．
已知数列{an}满足an+1=2an+3×2n+1，且a1=-20，
（Ⅰ）求证：数列{
an
2n
}为等差数列，并求出数列{an}的通项公式．
（Ⅱ）求数列{an}的前n项和Sn．
（理）椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点分别为F1（-c，0），F2（c，0）．过左焦点F1弦AB的端点A(m，
3
)、B(n，-
3
3
5
)，△ABF2的内切圆半径为
2
3
5
，则椭圆方程离心率为
 
．
已知函数f（x）=
2x+3
3x
，数列{an}满足a1=1，an+1=f（
1
an
），n∈N*，
（1）求数列{an}的通项公式；
（2）令Tn=a1a2-a2a3+a3a4-a4a5+…-a2na2n+1，求Tn；
（3）令bn=
1
an-1an
 （n≥2），b1=3，sn=b1+b2+…+bn，若sn＜
m-2005
2
对一切n∈N+成立，求最小正整数m．
函数f（x）=
x+1
-
1-x
的最小值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网