Question

已知方程x³+2ax²+3bx+c=0（a，b，c∈R）的三个实根可分别作为一椭圆，一双曲线、一抛物线的离心率，则

a2+b2

的取值范围是（　　）

• A、(

  10

  3

  ，+∞)
• B、[

  10

  3

• C、(

  10

  ，+∞)
• D、[

  10

  ，+∞)

Answer 1

考点：圆锥曲线的综合,函数的零点,函数的零点与方程根的关系,函数在某点取得极值的条件

专题：导数的综合应用,圆锥曲线的定义、性质与方程

分析：利用抛物线的离心率为1，求出c=-1-2a-3b，分解函数的表达式为一个一次因式与一个二次因式的乘积，通过函数的零点即可推出a，b的关系，求解a²+b²的取值范围即可．

解答： 解：设f（x）=x³+2ax²+3bx+c，由抛物线的离心率为1，可知f（1）=1+2a+3b+c=0，故c=-1-2a-3b，
所以f（x）=（x-1）[x²+（2a+1）x+（2a+3b+1）]的另外两个根分别是一个椭圆一个双曲线的离心率，
故g（x）=x²+（2a+1）x+（2a+3b+1），有两个分别属于（0，1），（1，+∞）的零点，
故有g（0）＞0，g（1）＜0，即2a+3b+1＞0且4a+3b+3＜0，
则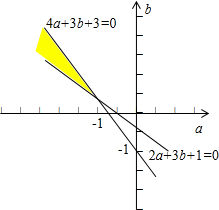a，b满足的可行域如图所示，
由于

2a+3b+1=0 4a+3b+3=0

，则P（-1，

1

3

）
而

a2+b2

表示（a，b）到（0，0）的距离，
且（0，0）到P（-1，

1

3

）的距离为d=

(-1)2+( 1 3 )2

=

10

3

可确定

a2+b2

的取值范围是（

10

3

，+∞）．
故答案为：A．

点评：本题考查一元二次方程的根的分布与系数的关系，简单线性规划，考查计算能力．