题目内容
已知loga
＜1，则a的取值范围是（ ）
| 2 |
| 5 |
A、0＜a＜
| ||
B、a＜
| ||
C、
| ||
D、0＜a＜
|
考点：指、对数不等式的解法
专题：函数的性质及应用,不等式的解法及应用
分析：因为底数a的范围不确定，故对底数a分类讨论，确定函数的单调性，将常数1化成logaa，再根据对数的单调性，求解即可得到a的取值范围．
解答：
解：loga
＜1=logaa，
当a＞1时，y=logax在（0，+∞）上单调递增，
则a＞
，∴a＞1；
当0＜a＜1时，y=logax在（0，+∞）上单调递减，
则a＜
，∴0＜a＜
，
综上所述：a的取值范围是0＜a＜
或a＞1．
故选D．
| 2 |
| 5 |
当a＞1时，y=logax在（0，+∞）上单调递增，
则a＞
| 2 |
| 5 |
当0＜a＜1时，y=logax在（0，+∞）上单调递减，
则a＜
| 2 |
| 5 |
| 2 |
| 5 |
综上所述：a的取值范围是0＜a＜
| 2 |
| 5 |
故选D．
点评：本题主要考查了对数不等式的解法，一般将底数化成相同再根据单调性进行求解，同时考查了分类讨论的数学思想，属于基础题．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
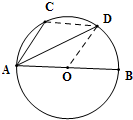
一个正三棱柱的三视图如图所示，则a=如图，AB是⊙O的直径，点C，D是半圆弧AB的两个三等分点，
=
，
=
，则
=（ ）
| AB |
| a |
| AC |
| b |
| AD |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知方程x3+2ax2+3bx+c=0（a，b，c∈R）的三个实根可分别作为一椭圆，一双曲线、一抛物线的离心率，则
的取值范围是（ ）
| a2+b2 |
A、(
| ||||
B、[
| ||||
C、(
| ||||
D、[
|
如图△ABC的三个顶点都在⊙O上，∠BAC的平分线与BC边和⊙O分别交于点D、E．