题目内容
已知离散型随机变量X的分布列为
且E（X）=1.5，则a-b= ．
| X | 1 | 2 | 3 |
| P | a | b | 0.1 |
考点：离散型随机变量的期望与方差,离散型随机变量及其分布列
专题：概率与统计
分析：根据离散型随机变量的概率分布列的性质、E（X）的定义，结合题意可得a+b+0.1=1，a+2b+3×0.1=1.5，由此求得a、b的值，可得a-b的值．
解答：
解：由离散型随机变量的概率分布列的性质、E（X）的定义可得 a+b+0.1=1，a+2b+3×0.1=1.5，
解得 a=0.6，b=0.3，
∴a-b=0.3，
故答案为 0.3．
解得 a=0.6，b=0.3，
∴a-b=0.3，
故答案为 0.3．
点评：本题主要考查离散型随机变量的概率分布列的性质、E（X）的定义，属于中档题．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
已知关于x的不等式ax2-ax-2a2＞1(a＞0且a≠1)的解集为{x|-a＜x＜2a}；且函数f(x)=
的定义域为R，则m的范围为（ ）
(
|
| A、[-1，0] | B、（0，1） |
| C、（1，+∞） | D、φ |
一个正三棱柱的三视图如图所示，则a=不等式
≥3的解集为 （ ）
| 2x+1 |
| x |
| A、[-1，0） |
| B、[-1，+∞） |
| C、（0，1] |
| D、（-∞，-1]∪（0，+∞） |
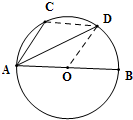
如图，AB是⊙O的直径，点C，D是半圆弧AB的两个三等分点，
=
，
=
，则
=（ ）
| AB |
| a |
| AC |
| b |
| AD |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知方程x3+2ax2+3bx+c=0（a，b，c∈R）的三个实根可分别作为一椭圆，一双曲线、一抛物线的离心率，则
的取值范围是（ ）
| a2+b2 |
A、(
| ||||
B、[
| ||||
C、(
| ||||
D、[
|
