题目内容
函数f(x)=sin(ωx-
)(0<ω<4)图象的一条对称轴方程是x=
,将函数f(x)的图象沿x轴向左平移
得到函数g(x)的图象,则函数g(x)的解析式是( )
| π |
| 3 |
| 5π |
| 12 |
| π |
| 6 |
| A、g(x)=sin2x | ||||
B、g(x)=sin(2x-
| ||||
C、g(x)=sin(
| ||||
D、g(x)=sin(
|
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:由三角函数的对称轴可得ω的值,再由函数图象的平移规律和三角函数公式可得答案.
解答:
解:∵f(x)=sin(ωx-
)图象的一条对称轴为x=
,
∴ω×
-
=kπ+
,k∈Z,可解得ω=
+2,
∵0<ω<4,∴只有当k=0时,ω=2符合题意,
∴f(x)=sin(2x-
),
又将函数f(x)的图象沿x轴向左平移
得到函数g(x)的图象,
∴g(x)=sin[2(x+
)-
]=sin2x
故选:A
| π |
| 3 |
| 5π |
| 12 |
∴ω×
| 5π |
| 12 |
| π |
| 3 |
| π |
| 2 |
| 12k |
| 5 |
∵0<ω<4,∴只有当k=0时,ω=2符合题意,
∴f(x)=sin(2x-
| π |
| 3 |
又将函数f(x)的图象沿x轴向左平移
| π |
| 6 |
∴g(x)=sin[2(x+
| π |
| 6 |
| π |
| 3 |
故选:A
点评:本题考查三角函数的解析式和图象的关系,属基础题.

练习册系列答案
相关题目
若tanα=1,则
的值为( )
| 2sinα+cosα |
| sinα-2cosα |
| A、1 | B、3 | C、-1 | D、-3 |
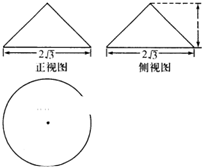
某几何体的三视图如图所示,则该几何体外接球的表面积为( )

A、
| ||
B、
| ||
| C、4π | ||
| D、16π |
某科室派出4名调研员到3个学校,调研高三复习备考近况,要求每个学校至少一名,则不同的分配方案的种数是( )
| A、144 | B、72 | C、36 | D、48 |
 某程序框图如图所示,现输入下列四个函数:f(x)=
某程序框图如图所示,现输入下列四个函数:f(x)=| 1 |
| x |
A、f(x)=
| ||
| B、f(x)=log3(x2+1) | ||
| C、f(x)=2x+2-x | ||
| D、f(x)=2x-2-x |
已知角α的终边经过点P(m,4),且cosα=-
,则m等于( )
| 3 |
| 5 |
A、-
| ||
| B、-3 | ||
C、
| ||
| D、3 |
已知等差数列{an},a2+a18=36,则a5+a6+…+a15=( )
| A、130 | B、198 |
| C、180 | D、156 |