题目内容

已知等差数列{an}，a2+a18=36，则a5+a6+…+a15=（　　）
A、130B、198
C、180D、156
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：利用等差数列的性质，求出a10=18，再利用a5+a6+…+a15=11a10，可得结论．
解答： 解：∵等差数列{an}，a2+a18=36，
∴2a10=36，
∴a10=18，
∴a5+a6+…+a15=11a10=198．
故选：B．
点评：本题考查等差数列的性质，灵活运用等差数列的性质是解本题的关键．
练习册系列答案
相关题目
执行如图所示的程序框图，若输出i的值为2，则输入x的最大值是（　　）
A、6B、12C、22D、24
函数f（x）=sin（ωx-
π
3
）（0＜ω＜4）图象的一条对称轴方程是x=
5π
12
，将函数f（x）的图象沿x轴向左平移
π
6
得到函数g（x）的图象，则函数g（x）的解析式是（　　）
A、g（x）=sin2x
B、g（x）=sin（2x-
π
6
）
C、g（x）=sin（
4
5
x-
π
6
）
D、g（x）=sin（
4
5
x-
π
30
）
下列结论正确的是（　　）
A、若向量
a
∥
b
，则存在唯一的实数λ使
a
=λ
b
B、已知向量
a
，
b
为非零向量，则“
a
，
b
的夹角为钝角”的充要条件是“
a
•
b
＜0’’
C、“若θ=
π
3
，则cosθ=
1
2
”的否命题为“若θ≠
π
3
，则cosθ≠
1
2
”
D、若命题p：?x∈R，x2-x+1＜0，则￢p：?x∈R，x2-x+1＞0
已知函数f（x）=
1
2
x2+（a-1）x+3在区间（-∞，4]上单调递减，则a的取值范围（　　）
A、[-3，+∞）
B、（-3，+∞）
C、（-∞，-3）
D、（-∞，-3]
已知a，b，c均为正实数，且ab+bc+ca=1．
求证：（Ⅰ）a+b+c≥
3
；
（Ⅱ）
a
bc
+
b
ca
+
c
ab
≥
3
（
a
+
b
+
c
）．
已知二次函数f（x）满足条件f（0）=2及f（x+1）-f（x）=2x，求：
（1）求f（x）；    
（2）求f（x）在区间[-1，2]上的最大值和最小值．
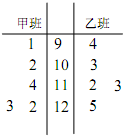为了解甲、乙两个班级某次考试的数学成绩（单位：分），从甲、乙两个班级中分别随机抽取5名学生的成绩作样本，如图是样本的茎叶图．规定：成绩不低于120分时为优秀成绩．
（1）从甲班的样本中有放回的随机抽取 2 个数据，求其中只有一个优秀成绩的概率；
（2）从甲、乙两个班级的样本中分别抽取2名同学的成绩，记获优秀成绩的人数为ξ，求ξ的分布列和数学期望Eξ．
已知函数f（x）=x2+ax+2ln（x-1），a是常数．
（1）若a=1，求y=f（x）在点（2，f（2））处的切线方程；
（2）若f′（x）＞（a-3）x2对?x∈（2，3）恒成立，求a的取值范围．
（参考公式：3x3-x2-2x+2=（x+1）（3x2-4x+2））

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网