题目内容
11.已知项数为2n+1的等差数列{an}满足a1+a2n+1≠0,所有奇数项的和为S奇,所有偶数项的和为S偶,则$\frac{{S}_{奇}}{{S}_{偶}}$的值为$\frac{n+1}{n}$.分析 利用等差数列的通项公式性质及其前n项和公式即可得出.
解答 解:等差数列{an}满足a1+a2n+1≠0,
所有奇数项的和为S奇=$\frac{(n+1)({a}_{1}+{a}_{2n+1})}{2}$=(n+1)an+1;
所有偶数项的和为S偶=$\frac{n({a}_{2}+{a}_{2n})}{2}$=nan+1≠0.
则$\frac{{S}_{奇}}{{S}_{偶}}$=$\frac{n+1}{n}$,
故答案为:$\frac{n+1}{n}$.
点评 本题考查了等差数列的通项公式性质及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.直角梯形ABCD满足AB∥CD,AD=CD=$\frac{1}{2}$AB=1,AD⊥AB,点M是梯形边上的任意一点.则AM≥$\sqrt{2}$的概率是( )
| A. | $\frac{4+\sqrt{2}}{7}$ | B. | $\frac{4-\sqrt{2}}{7}$ | C. | $\frac{4+\sqrt{2}}{8}$ | D. | $\frac{4-\sqrt{2}}{8}$ |
6.sin20°cos40°+sin70°sin140°的值等于( )
| A. | $\frac{1}{4}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{4}$ |
1.某校高三数学备课组为了更好的制定二轮复习的计划,开展了试卷讲评后效果的调研,从上学期期末数学试题中选出一些学生易错题.重新进行测试,并认为做这些题不出任何错误的同学为“过关”,出了错误的同学认为“不过关”,现随机调查了年级50人,他们的测试成绩的频数分别如表:
(1)由以上统计数据完成如下2×2列联表,并判断是否有95%的把认为期末数学成绩不低于90分与测试“过关”有关?说明你的理由.
(2)在期末分数段[105,120)的5人中,从中随机选3人,记抽取到过关测试“过关”的人数为X,求X的分布列及数学期望.
下面的临界值表供参考:
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
| 期末分数段 | (0,60) | [60,75) | [75,90) | [90,105) | [105,120) | [120,150] |
| 人数 | 5 | 10 | 15 | 10 | 5 | 5 |
| “过关”人数 | 1 | 2 | 9 | 7 | 3 | 4 |
| 分数低于90分人数 | 分数不低于90分人数 | 合计 | |
| 过关人数 | |||
| 不过关人数 | |||
| 合计 |
下面的临界值表供参考:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 |
| K | 2.072 | 2.706 | 3.841 | 5.024 |
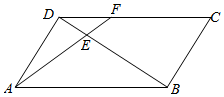 如图,点E是平行四边形ABCD对角线BD的4等分点中最靠近点D的那个分点,线段AE的延长线交CD于点F,若|$\overrightarrow{AB}$|=2,|$\overrightarrow{AD}$|=1,<$\overrightarrow{AB}$,$\overrightarrow{AD}$>=60°,则$\overrightarrow{AF}$•$\overrightarrow{AD}$的值为$\frac{4}{3}$.
如图,点E是平行四边形ABCD对角线BD的4等分点中最靠近点D的那个分点,线段AE的延长线交CD于点F,若|$\overrightarrow{AB}$|=2,|$\overrightarrow{AD}$|=1,<$\overrightarrow{AB}$,$\overrightarrow{AD}$>=60°,则$\overrightarrow{AF}$•$\overrightarrow{AD}$的值为$\frac{4}{3}$.