题目内容
19.在△ABC中,a,b,c分别是角A,B,C所对的边,cos2B-$\sqrt{3}$cos(A+C)=2.(1)求角B的大小;
(2)若b=2,求AC边上高h的最大值.
分析 (1)使用二倍角公式计算cosB;
(2)利用余弦定理求出ac的最大值,根据三角形的面积求出高.
解答 解:(I)在△ABC中,∵cos2B-$\sqrt{3}$cos(A+C)=2,
∴2cos2B-1+$\sqrt{3}$cosB=2,解得cosB=$\frac{\sqrt{3}}{2}$或cosB=-$\sqrt{3}$(舍).
∴B=$\frac{π}{6}$.
(2)由余弦定理得cosB=$\frac{{a}^{2}+{c}^{2}-4}{2ac}=\frac{\sqrt{3}}{2}$,
∴a2+c2=4+$\sqrt{3}$ac≥2ac,解得ac≤4(2+$\sqrt{3}$).
∴S=$\frac{1}{2}acsinB$=$\frac{1}{4}ac$≤2+$\sqrt{3}$.
又∵S=$\frac{1}{2}bh$≤2+$\sqrt{3}$,∴h≤2+$\sqrt{3}$.
∴AC边上高h的最大值为2+$\sqrt{3}$.
点评 本题考查了三角函数的恒等变换,余弦定理在解三角形中的应用,属于中档题.

练习册系列答案
相关题目
9.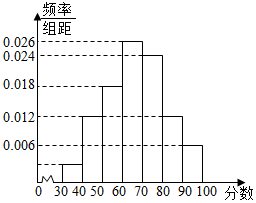 某校高二年级共有1600名学生,其中男生960名,640名,该校组织了一次满分为100分的数学学业水平模拟考试,根据研究,在正式的学业水平考试中,本次成绩在[80,100]的学生可取得A等(优秀),在[60,80)的学生可取得B等(良好),在[40,60)的学生可取得C等(合格),在不到40分的学生只能取得D等(不合格),为研究这次考试成绩优秀是否与性别有关,现按性别采用分层抽样的方法抽取100名学生,将他们的成绩按从低到高分成[30,40)、[40,50)、[50,60)、[60,70)、[70,80)、[80,90)、[90,100]七组加以统计,绘制成频率分布直方图,如图是该频率分布直方图.
某校高二年级共有1600名学生,其中男生960名,640名,该校组织了一次满分为100分的数学学业水平模拟考试,根据研究,在正式的学业水平考试中,本次成绩在[80,100]的学生可取得A等(优秀),在[60,80)的学生可取得B等(良好),在[40,60)的学生可取得C等(合格),在不到40分的学生只能取得D等(不合格),为研究这次考试成绩优秀是否与性别有关,现按性别采用分层抽样的方法抽取100名学生,将他们的成绩按从低到高分成[30,40)、[40,50)、[50,60)、[60,70)、[70,80)、[80,90)、[90,100]七组加以统计,绘制成频率分布直方图,如图是该频率分布直方图.
(Ⅰ)估计该校高二年级学生在正式的数学学业水平考试中,成绩不合格的人数;
(Ⅱ) 请你根据已知条件将下列2×2列联表补充完整,并判断是否有90%的把握认为“该校高二年级学生在本次考试中数学成绩优秀与性别有关”?
附:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$.
 某校高二年级共有1600名学生,其中男生960名,640名,该校组织了一次满分为100分的数学学业水平模拟考试,根据研究,在正式的学业水平考试中,本次成绩在[80,100]的学生可取得A等(优秀),在[60,80)的学生可取得B等(良好),在[40,60)的学生可取得C等(合格),在不到40分的学生只能取得D等(不合格),为研究这次考试成绩优秀是否与性别有关,现按性别采用分层抽样的方法抽取100名学生,将他们的成绩按从低到高分成[30,40)、[40,50)、[50,60)、[60,70)、[70,80)、[80,90)、[90,100]七组加以统计,绘制成频率分布直方图,如图是该频率分布直方图.
某校高二年级共有1600名学生,其中男生960名,640名,该校组织了一次满分为100分的数学学业水平模拟考试,根据研究,在正式的学业水平考试中,本次成绩在[80,100]的学生可取得A等(优秀),在[60,80)的学生可取得B等(良好),在[40,60)的学生可取得C等(合格),在不到40分的学生只能取得D等(不合格),为研究这次考试成绩优秀是否与性别有关,现按性别采用分层抽样的方法抽取100名学生,将他们的成绩按从低到高分成[30,40)、[40,50)、[50,60)、[60,70)、[70,80)、[80,90)、[90,100]七组加以统计,绘制成频率分布直方图,如图是该频率分布直方图.(Ⅰ)估计该校高二年级学生在正式的数学学业水平考试中,成绩不合格的人数;
(Ⅱ) 请你根据已知条件将下列2×2列联表补充完整,并判断是否有90%的把握认为“该校高二年级学生在本次考试中数学成绩优秀与性别有关”?
| 数学成绩优秀 | 数学成绩不优秀 | 合计 | |
| 男生 | a=12 | b= | |
| 女生 | c= | d=34 | |
| 合计 | n=100 |
| P(k2≥k0) | 0.15 | 0.10 | 0.05 |
| k0 | 2.072 | 2.706 | 3.841 |
7.在等比数列{an}中,已知a2+a3=1,a3+a4=$\sqrt{2}$,则a14+a15等于( )
| A. | 16 | B. | 32 | C. | 64 | D. | 128 |
9.某超市某种面包进货价为每个4元,实际售价为每个4.5元,若当天不能卖完,就在闭店前以每个3元的价格全部处理,据以往统计日需求量(单位:个)的情况如表:
若某日超市面包进货量为600.
(1)若以日需求量x所在区间的中间值为估计值,根据上表列出当日利润y的分布列;
(2)估计超市当日利润y的均值.
| 日需求量x | (0,400] | (400,600] | (600,800] | (800,1000] |
| 频率 | 0.2 | 0.4 | 0.3 | 0.1 |
(1)若以日需求量x所在区间的中间值为估计值,根据上表列出当日利润y的分布列;
(2)估计超市当日利润y的均值.