题目内容
1.某校高三数学备课组为了更好的制定二轮复习的计划,开展了试卷讲评后效果的调研,从上学期期末数学试题中选出一些学生易错题.重新进行测试,并认为做这些题不出任何错误的同学为“过关”,出了错误的同学认为“不过关”,现随机调查了年级50人,他们的测试成绩的频数分别如表:| 期末分数段 | (0,60) | [60,75) | [75,90) | [90,105) | [105,120) | [120,150] |
| 人数 | 5 | 10 | 15 | 10 | 5 | 5 |
| “过关”人数 | 1 | 2 | 9 | 7 | 3 | 4 |
| 分数低于90分人数 | 分数不低于90分人数 | 合计 | |
| 过关人数 | |||
| 不过关人数 | |||
| 合计 |
下面的临界值表供参考:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 |
| K | 2.072 | 2.706 | 3.841 | 5.024 |
分析 (I)依题意求出a、b、c、d的值,填写列联表;计算观测值K2,对照数表得出概率结论;
(II)求出在期末分数段[105,120)的5人中随机选3人,“过关”人数X的分布列与数学期望.
解答 解:(I)依题意得,a=12,b=18,c=14,d=6,
填写列联表如下;
| 分数低于9(0分)人数 | 分数高于9(0分)人数 | 合计 | |
| 过关人数 | 12 | 14 | 26 |
| 不过关人数 | 18 | 6 | 24 |
| 合计 | 30 | 20 | 50 |
对照数表知,有95%的把握认为期末数学成绩不低于90(分)与测试“过关”有关;(6分)
(II)在期末分数段[105,120)的5人中,有3人 测试“过关”,
随机选3人,抽取到过关测试“过关”的人数为X的可能取值为1、2、3,
则P(X=1)=$\frac{{C}_{2}^{2}{•C}_{3}^{1}}{{C}_{5}^{3}}$=$\frac{3}{10}$,
P(X=2)=$\frac{{C}_{2}^{1}{•C}_{3}^{2}}{{C}_{5}^{3}}$=$\frac{6}{10}$,
P(X=3)=$\frac{{C}_{3}^{3}}{{C}_{5}^{3}}$=$\frac{1}{10}$,
所以,X的分布列为:
| X | 1 | 2 | 3 |
| P | $\frac{3}{10}$ | $\frac{6}{10}$ | $\frac{1}{10}$ |
点评 本题考查了离散型随机变量的分布列与数学期望的应用问题,也考查了独立性检验的应用问题,是基础题.

练习册系列答案
相关题目
9.某超市某种面包进货价为每个4元,实际售价为每个4.5元,若当天不能卖完,就在闭店前以每个3元的价格全部处理,据以往统计日需求量(单位:个)的情况如表:
若某日超市面包进货量为600.
(1)若以日需求量x所在区间的中间值为估计值,根据上表列出当日利润y的分布列;
(2)估计超市当日利润y的均值.
| 日需求量x | (0,400] | (400,600] | (600,800] | (800,1000] |
| 频率 | 0.2 | 0.4 | 0.3 | 0.1 |
(1)若以日需求量x所在区间的中间值为估计值,根据上表列出当日利润y的分布列;
(2)估计超市当日利润y的均值.
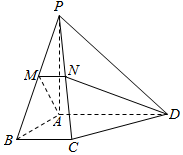 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,PA=AD=AB=2BC=2,过AD的平面分别交PB,PC于M,N两点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,PA=AD=AB=2BC=2,过AD的平面分别交PB,PC于M,N两点.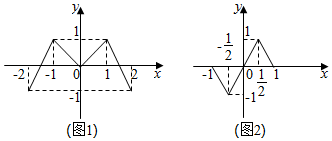 已知偶函数f(x),奇函数g(x)的图象分别如图(1)、图(2)所示,若f(y0)=0且y0=g(x0),则x0的值为-1,0,或1.
已知偶函数f(x),奇函数g(x)的图象分别如图(1)、图(2)所示,若f(y0)=0且y0=g(x0),则x0的值为-1,0,或1. 某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,并得到如图的频率分布直方图.
某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,并得到如图的频率分布直方图.