题目内容
已知f(x)=x2+bx+c为偶函数,曲线y=f(x)过点(2,5),g(x)=(x+a)f(x),g(x)的导函数为g′(x)
(Ⅰ)若曲线y=g(x)有斜率为0的切线,求实数a的取值范围;
(Ⅱ)若g′(-1)=0,求y=g(x)的单调区间.
(Ⅰ)若曲线y=g(x)有斜率为0的切线,求实数a的取值范围;
(Ⅱ)若g′(-1)=0,求y=g(x)的单调区间.
考点:二次函数的性质
专题:函数的性质及应用,导数的概念及应用,导数的综合应用
分析:(Ⅰ)据偶函数的定义f(-x)=f(x)求出b值,将点(2,5)代入得c值,据导数在切点处的导数值为切线斜率,有g′(x)=0有实数解,由△≥0得范围.
(Ⅱ)函数在极值点处的导数值为0,导数大于0对应区间是单调递增区间;导数小于0对应区间是单调递减区间.
(Ⅱ)函数在极值点处的导数值为0,导数大于0对应区间是单调递增区间;导数小于0对应区间是单调递减区间.
解答:
解:(Ⅰ)∵f(x)=x2+bx+c为偶函数,故f(-x)=f(x),
即有(-x)2+b(-x)+c=x2+bx+c,解得b=0,
又曲线y=f(x)过点(2,5),得22+c=5,有c=1,
∵g(x)=(x+a)f(x)=x3+ax2+x+a,
从而g′(x)=3x2+2ax+1,
∵曲线y=g(x)有斜率为0的切线,故有g′(x)=0有实数解.
即3x2+2ax+1=0有实数解.
此时有△=4a2-12≥0解得
a∈(-∞,-
]∪[
,+∞)
所以实数a的取值范围:a∈(-∞,-
]∪[
,+∞);
(Ⅱ)因x=-1时函数y=g(x)取得极值,故有g′(-1)=0,即3-2a+1=0,解得a=2
又g′(x)=3x2+4x+1=(3x+1)(x+1),
令g′(x)=0,得x1=-1,x2=-
,
当x∈(-∞,-1)时,g′(x)>0,故g(x)在(-∞,-1)上为增函数,
当x∈(-1,-
)时,g′(x)<0,故g(x)在(-1,-
)上为减函数,
当x∈(-
,+∝)时,g′(x)>0,故g(x)在(-
,+∝)上为增函数.
即有(-x)2+b(-x)+c=x2+bx+c,解得b=0,
又曲线y=f(x)过点(2,5),得22+c=5,有c=1,
∵g(x)=(x+a)f(x)=x3+ax2+x+a,
从而g′(x)=3x2+2ax+1,
∵曲线y=g(x)有斜率为0的切线,故有g′(x)=0有实数解.
即3x2+2ax+1=0有实数解.
此时有△=4a2-12≥0解得
a∈(-∞,-
| 3 |
| 3 |
所以实数a的取值范围:a∈(-∞,-
| 3 |
| 3 |
(Ⅱ)因x=-1时函数y=g(x)取得极值,故有g′(-1)=0,即3-2a+1=0,解得a=2
又g′(x)=3x2+4x+1=(3x+1)(x+1),
令g′(x)=0,得x1=-1,x2=-
| 1 |
| 3 |
当x∈(-∞,-1)时,g′(x)>0,故g(x)在(-∞,-1)上为增函数,
当x∈(-1,-
| 1 |
| 3 |
| 1 |
| 3 |
当x∈(-
| 1 |
| 3 |
| 1 |
| 3 |
点评:本题考查偶函数的定义;利用导数几何意义求曲线切线方程;利用导数求函数单调区间.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数y=
+
是( )
| 1-x2 |
| 2 |
| 1+|x| |
| A、奇函数 |
| B、偶函数 |
| C、既是奇函数又是偶函数 |
| D、非奇非偶函数 |
甲、乙两人参加一次射击游戏,规则规定,每射击一次,命中目标得2分,未命中目标得0分.已知甲、乙两人射击的命中率分别为
和p,且甲、乙两人各射击一次所得分数之和为2的概率是
.假设甲、乙两人射击是相互独立的,则p的值为( )
| 3 |
| 5 |
| 9 |
| 20 |
A、
| ||
B、
| ||
C、
| ||
D、
|
当点(x,y)在直线x+3y=2上移动时,u=3x+27y+1的最小值是( )
| A、7 | |||
B、3
| |||
C、1+2
| |||
| D、6 |
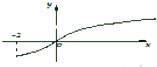 已知f(x)的定义域为[-2,+∞),部分对应值如下表,f′(x)为f(x)的导函数,函数y=f′(x)的图象如图,若f(x)<1,则x的范围为
已知f(x)的定义域为[-2,+∞),部分对应值如下表,f′(x)为f(x)的导函数,函数y=f′(x)的图象如图,若f(x)<1,则x的范围为